Caucher Birkar, người tị nạn đem lại trật tự cho vô hạn phương trình

Nhà toán học Caucher Birkar sinh ra ở một trang trại tự cung tự cấp và lớn lên trong cuộc chiến tranh khốc liệt giữa Iran và Iraq. Sau khi tới Anh, anh tìm cách áp đặt một trật tự cho sự hỗn loạn của các phương trình toán học.

Caucher ngồi trong vườn nhà anh gần Cambridge, Anh.

Mùa xuân này, không lâu sau khi Caucher Birkar biết rằng mình sẽ được trao Huân chương Fields, giải thưởng danh giá bậc nhất trong toán học, anh đã chia sẻ một kỷ niệm từ thời còn là sinh viên. Ngay cả khi ấy anh cũng đã trải qua một quãng đường dài. Sinh ra và lớn lên ở một vùng ngoại ô của một làng nông nghiệp tự cung tự cấp ở vùng người Kurd ở Tây Iran, Birkar thi đỗ vào Đại học Tehran, một trong những đại học lớn nhất của đất nước anh. Ở đó, tại câu lạc bộ toán học, anh hồi tưởng lại lúc nhìn ảnh các nhà toán học được giải thưởng Fields treo trên tường. “Tôi nhìn vào họ và tự nói với mình, ‘Có khi nào mình được gặp một trong số họ không nhỉ?’ Khi đó ở Iran, tôi thậm chí còn không biết được rằng mình có thể tới được phương Tây”.

Có nhiều chuyện trong tương lai của mình mà Birkar đã không thể dự đoán vào thời điểm đó: chuyến bay của anh rời khỏi Iran, lời thỉnh cầu xin tị nạn chính trị của anh, nỗ lực thắp lại một ngành toán học gần như bị bỏ quên. Và hôm nay, trong một buổi lễ ở Rio de Janeiro, anh vinh dự được lựa chọn là một trong bốn người được trao Huân chương Fields, một giải thưởng được Hội Toán học Quốc tế trao bốn năm một lần cho các nhà toán học tài năng nhất trên thế giới chưa quá 40 tuổi vào đầu năm trao giải. “Để đi từ điểm mà tôi không tưởng tượng nổi, là được gặp những người đó rồi tới một ngày cầm huy chương này trên tay – tôi chỉ không thể tin nổi đó lại là sự thật”, Birkar, người tròn 40 tuổi vào tháng 7 này, nói.

Là một nhà toán học, Birkar đã giúp mang lại trật tự cho họ vô hạn các phương trình đa thức – những phương trình nhiều biến với bậc đa dạng. Không có hai phương trình nào giống hệt nhau, nhưng Birkar đã khám phá ra rằng có thể phân loại nhiều phương trình trong số đó vào các họ nhỏ hơn. Trong hai bài báo công bố năm 2016, anh đã chỉ ra rằng có thể xác định một số vô hạn các phương trình bằng một số đặc trưng hữu hạn – một kết quả đã chứng tỏ rằng mảng rối rắm các phương trình đại số dường như chẳng liên quan gì tới nhau lại có một số điểm chung.

Công  trình gần đây của Birkar về các đa tạp Fano là một trong những kết quả toán học giàu sức ảnh hưởng nhất của anh, nhưng nó nảy sinh từ một niềm thôi thúc đã chi phối anh kể từ khi bắt đầu tự học toán ba thập kỷ trước: mong muốn thôi thúc tạo ra thứ gì đó mới mẻ.

Cuộc cách mạng đầu tiên

Khi Birkar còn rất nhỏ, anh thích ở gần mẹ, Sakina, trong khi bà nướng bánh mỳ. Bà còn nhớ một lần khi Birkar lên ba. “Nó ngồi cạnh tôi, cố gắng lại thật gần, cố gắng để chạm chân vào chân tôi”, bà kể.

Mẹ của Birkar đã kể tôi nghe câu chuyện này qua Skype. Khi đó, anh ta và tôi đang ngồi trong phòng khách của căn nhà nhỏ của anh ở Cambourne, một khu dân cư cách Cambridge, Anh, 10 dặm, được xây từ hai thập kỷ trước. Mẹ anh đang sống ở Marivan, một làng người Kurd trong một vùng núi gần biên giới Iran-Iraq nơi nhiều thế hệ gia đình Birkar đã sống. Bà đội một chiếc mũ len trắng và đang ngồi trên trường kỷ bên cạnh anh cả và cha của Birka, Majid.

Caucher Birkar sinh năm 1978, là con thứ ba trong sáu người con. Gia đình anh sống ở một trang trại gia đình, trồng lúa nước, lúa mỳ và rau củ. Họ cũng nuôi cừu và đôi khi cả ngựa. Gia đình đã tự cung tự cấp theo một cái cách giúp che chở cho Birkar khỏi những điều tồi tệ nhất của những ầm ĩ đã nhấn chìm cả khu vực trong suốt thời thơ ấu của anh– Cuộc Cách mạng Hồi giáo vào năm 1979 và 8 năm chiến tranh khốc liệt với Iraq không lâu sau đó.

“Không lâu sau khi tôi sinh ra đã có một cuộc cách mạng và chiến tranh, nhưng sự thật là chúng tôi đã sản xuất ra mọi thứ mình cần, nghĩa là chúng tôi có thể sống sót”, anh nói.

Văn phòng của Birkar ở Đại học Cambridge treo hình Alexander Grothedieck đang ngồi với một nhóm các nhà hoạt động. Nguồn: Kevin Hartnett

Cha của Birkar chỉ đến trường học trong vài năm. Mẹ anh không được chính thức theo học ở đâu cả. Nhưng Birkar và anh em ruột thì được theo học ở trường làng. Tới khoảng lớp 5, Birkar đã bắt đầu chú ý tới toán học. “Tôi có cảm nhận gì đó. Không có gì nghiêm túc, đó chỉ là một cảm nhận thoáng qua rằng tôi học tốt toán”, anh kể lại.

Ngay từ buổi đầu, người nắm giữ niềm ưa thích toán học của Birkar là Haidar, anh cả của anh, người đã giới thiệu cho Birkar các khái niệm cơ sở của giải tích. “Cậu ấy rất tò mò với những vấn đề toán học và vật lý”. Haidar nói qua Skype. “Tôi còn nhớ cậu ấy đã cầm sách bài tập của tôi và cố gắng giải các bài toán trong đó”.

Birkar nhớ rằng người anh trai còn dạy anh điều gì đó khác nữa, là: hiểu biết có thể rất tinh tế.

“Anh ấy có lẽ là người duy nhất tôi biết, người theo đuổi đam mê của mình, không chỉ để có điểm cao ở trường. Anh ấy còn giỏi hơn thế nhiều, anh ấy thực sự ưa thích một số thứ nhất định”, Birkar kể lại. “Anh ấy đã làm những điều mà không ai dám làm ở môi trường đó”.

Tới phổ thông, Birkar đã có kiến thức toán học vượt trội hơn anh trai mình và tự học toán một mình. Anh mượn các cuốn sách từ thư viện địa phương với tựa đề như Những con người của toán học và Toán học là gì. Gia đình anh còn nhớ anh đã đọc sách tới khuya trong khi nghe nhạc – một thói quen mà tới nay anh vẫn còn giữ.

Ngay từ những tiếp xúc thoáng qua đầu tiên với toán học chuyên nghiệp, Birkar đã muốn làm nhiều hơn là chỉ ngưỡng mộ những khám phá của người khác. “Tôi đã đọc tất cả các cuốn sách và có được cảm nhận rằng chỉ đọc thôi thì không đủ. Tôi cũng muốn tạo ra những thứ của riêng mình, tạo ra cái gì đó mới”, anh kể.

Từ khi còn là một học sinh cấp ba anh đã bắt đầu viết ra những chứng minh toán học của riêng mình. Thời đại học, anh đã bắt đầu gửi chúng cho các tạp chí toán học. Về sau, khi đã được rèn luyện bài bản đôi chút, anh đã nhận ra các chứng minh mình tìm ra đã được khám phá từ rất lâu rồi. “Có lẽ tôi đã không chứng minh được cái gì đáng chú ý, nhưng kinh nghiệm và thái độ làm việc đó, đã cho thấy sự hữu ích trong những bước đường học tập sau này của tôi”, anh nói.

Birkar thi vào Đại học Tehran. Năm cuối đại học, anh tới Anh. Trong khi ở đó, anh xin tị nạn chính trị để tránh “các vấn đề chính trị ở Iran đối với những người như tôi”, anh kể lại, nhắc tới đặc tính Kurd của mình, một dân tộc thiểu số thường phải chịu sự đàn áp của các tổ chức mà nhà nước đỡ đầu. Chính phủ Anh đã cho anh tới Nottingham, một thành phố ở trung tâm nước Anh. Trong suốt một năm chính phủ xử lý trường hợp của anh, Birkar đã gặp các giáo sư khoa toán ở Đại học Nottingham, nơi anh theo học sau khi yêu cầu tị nạn được thông qua.

Không có ai ở Đại học Nottingham chuyên về hình học đại số, lĩnh vực mà Birkar muốn bước vào. Nhưng thầy hướng dẫn chính thức của Birkar ở đó, một nhà lý thuyết số tên là Ivan Fesenko, đã động viên anh tới tham dự các sự kiện toán học bên ngoài trường đại học. Trong một cuộc hội thảo năm 2002 ở Cambridge, Birkar đã gặp Vyacheslav Shokurov, một nhà toán học ở Đại học John Hopkins. Không lâu sau khi quen nhau, Shokurov đã đưa Birkar đi trượt tuyết vài giờ ở Baltimore. Shokurov ngạc nhiên trước tốc độ học môn thể thao này của Birkar và khả năng chịu đựng của anh.  

“Cậu ấy là một người nhút nhát và lịch sự, có lẽ, bởi vì cậu ấy lớn lên từ làng và trong một gia đình truyền thống”, Shokurov viết trong thư điện tử.

Khi gặp Birkar, Shokurov đã nghiên cứu nhiều năm ròng trong một ngành hẹp của hình học đại số gần như đã bị lãng quên gọi là hình học song hữu tỷ. Hình học song hữu tỷ đã có vài bước tiến quan trọng trong hơn một thập kỷ trước, nhưng ngành này đã dần chìm lắng vì thiếu vắng các ý tưởng mới. “Toàn bộ ngành này gần như đã chững lại. Hầu hết mọi người đều từ bỏ”, Birkar nói.

Shokurov là một trong một số rất ít nhà toán học không bỏ cuộc. Ở Birkar ông thấy một nhà toán học trẻ tuổi có khả năng tiếp thêm sinh khí cho ngành này.

Ba kiểu vô hạn

Tại phòng làm việc ở Đại học Cambridge, Birkar trưng hai bức ảnh của nhà toán học Alexander Grothendieck. Grothendieck là một người tị nạn – ông đã trốn chạy Đức Quốc xã – và cũng là một người được trao huân chương Fields, giống như Birkar. Ông cũng được coi là nhà toán học có ảnh hưởng nhất nửa sau thế kỷ 20. Trong một bức ảnh, Grothendieck ngồi với một nhóm các nhà hoạt động khác nhau tham gia vào phong trào bảo vệ môi trường ở Pháp vào đầu những năm 1970. Birkar, một người Kurd lớn lên ở Iran và giờ đây sống ở Anh, nơi anh cưới một phụ nữ Thái Lan, ngưỡng mộ cả hai khía cạnh của Grothendieck: tầm nhìn toán học của ông và cách ông hòa đồng với những người có gốc gác khác nhau.

“Tất cả những nền văn hóa này khiến tôi thấy mọi thứ thú vị hơn. Tất cả những nền văn hóa này mang lại cho bạn cảm nhận về sự viên mãn”, anh nói. Con trai bốn tuổi của anh, Zanko, là phản chiếu sống động của sự đa dạng này: cháu nói tiếng Thái gốc của mẹ, tiếng Kurd gốc của bố và tiếng Anh của nơi cháu sinh ra.

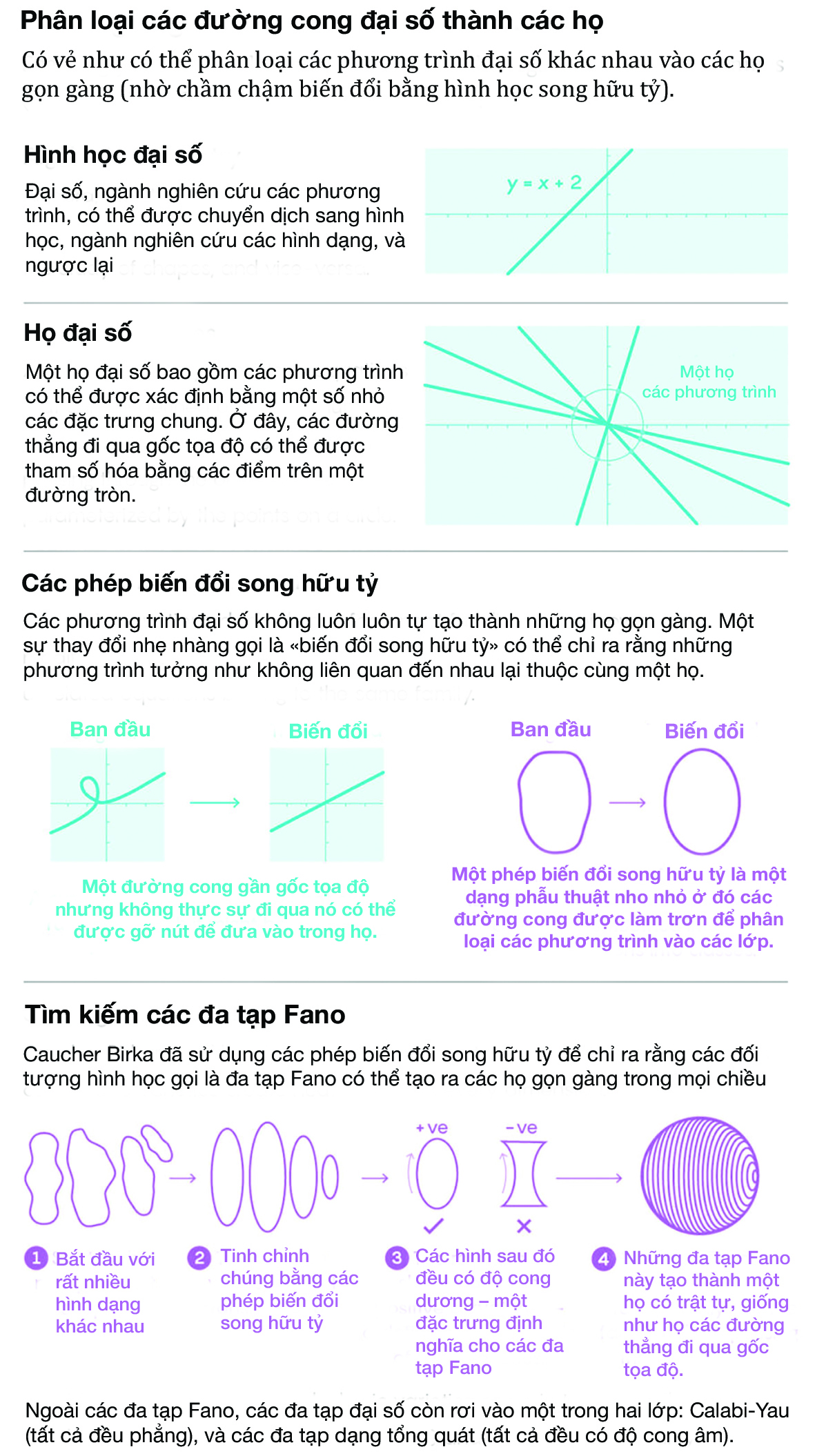
Hình học đại số cũng là một hỗn hợp của các nền văn hóa. Một mặt nó là đại số, lĩnh vực nghiên cứu các phương trình, và mặt khác nó lại là hình học, ngành nghiên cứu các hình dạng. Hai cách nhìn khác nhau cho cùng các vấn đề. Hãy xét phương trình đại số y=2x-3. Nếu vẽ đồ thị nghiệm của nó, bạn sẽ có một đối tượng hình học– một đường thẳng. Hai khía cạnh này bổ sung cho nhau. Nếu bạn muốn tìm nghiệm chung của hai phương trình, chẳng hạn y=2x-3 và y=3x+5, bạn có thể tìm nhờ đại số, hoặc bạn có thể vẽ đồ thị của hai phương trình và xem chúng cắt nhau ở đâu.  

“Đôi khi một câu hỏi hình học có thể được giải quyết bằng các phương pháp đại số và đôi khi một câu hỏi đại số có thể được giải quyết bằng các phương pháp hình học”, János Kollár, nhà toán học ở Đại học Princeton nói. “Bạn có thể dịch chuyển giữa hai đối tượng này và giúp cho chúng trở nên phong phú hơn”.

Các phương trình tuyến tính là những phương trình đại số đơn giản nhất. Ngoài ra, có rất nhiều kiểu phương trình đại số khác. Chúng có thể có nhiều biến hơn và những biến này có bậc khác nhau. Bạn cũng có thể nghĩ về tập hợp các nghiệm chung cho một nhóm các phương trình. Tập hợp này được gọi là một “đa tạp đại số”. Tồn tại vô hạn các đa tạp đại số; mỗi đa tạp lại có một biểu diễn hình học độc nhất.

“Điều quan trọng nhất là hình dạng, cấu trúc của tập nghiệm”, Birkar nói. “Tập nghiệm chính là cái chúng tôi đại khái gọi là đa tạp đại số”.

Các đa tạp đại số là một tập lỏng lẻo. Các nhà toán học muốn thiết lập trật tự cho chúng. Điều này cũng tương tự như việc chúng ta mong muốn phân loại các dạng sống sinh học – trí tuệ của chúng ta dường như dễ nhận biết thế giới sống hơn, và thấy hình dạng của nó có ý nghĩa hơn, nếu ta có thể xếp chúng theo từng ngành và họ thay vì gọi tên riêng của từng cá thể một.

Hình học song hữu tỷ là một cách biến đổi các đa tạp sao cho người ta có thể phân loại chúng. Đó là một kiểu phẫu thuật: Bạn bắt đầu với một đa tạp, vốn có kiểu bất thường riêng, sau đó cắt bỏ những khối lồi lõm của nó và làm phẳng các nếp nhăn, cho tới cuối cùng bạn có một dạng tổng quát hơn. Có một số giới hạn nghiêm ngặt cho những gì bạn được phép cắt bỏ, để đảm bảo rằng bạn không hoàn toàn xóa bỏ đa tạp ban đầu. Sau khi phẫu thuật, rất nhiều các đa tạp khác biệt trước đây giờ trông giống hệt; chúng được coi là cùng thuộc “lớp tương đương song hữu tỷ”.

“Chúng tôi đang tập trung vào bức tranh tổng thể và không bận tâm về sự khác biệt ở một tập hợp con nhỏ các điểm trên các đa tạp”, Christopher Hacon, nhà toán học ở Đại học Utah và một người dẫn đầu trong lĩnh vực hình học song hữu tỷ sẽ trình bày về công trình của Birkar tại lễ trao Huân chương Fields ở Rio, nói.

Có ba lớp tương đương song hữu tỷ rộng: các đa tạp Fano, đa tạp Calabi-Yau, và các đa tạp dạng tổng quát. Ba lớp này đều là các dạng tổng quát, giống y như thuật ngữ “côn trùng” là tổng quát so với các sinh vật cụ thể nằm dưới nó. Mỗi lớp lại có một độ cong nhất định (hoặc đều dương, hoặc đều âm, hoặc đều phẳng, tương ứng). Các nhà toán học hi vọng họ có thể chỉ ra rằng mỗi đa tạp có thể được giản lược về một trong ba dạng tổng quát này qua các phép biến đổi song hữu tỷ.

“Chúng tôi hi vọng tìm thấy các đối tượng có cùng kiểu độ cong ở khắp mọi nơi”, Kollár nói. “Chúng tôi không muốn một thứ, lúc thì giống mặt cầu, lúc thì giống mặt yên ngựa, lúc thì phẳng. Như thế thì quá phức tạp”.

Các điểm mang tới trật tự

Birkar đã tự mình hoàn thành những công trình toán học quan trọng nhất của bản thân trong phòng ăn. Một ngày bình thường, anh sẽ làm việc bên bàn, khởi động và suy nghĩ, pha trà, hay bật nhạc, thường là nhạc cổ điển hoặc các bài hát Kurd đương đại. “Rất nhiều bài hát đi vào tâm trí tôi. Đôi khi cả ngày tôi chỉ viết có một trang thôi”, anh nói. Sau vài giờ suy nghĩ anh thích thư giãn tâm trí bằng cách đạp xe dọc theo đường mòn quanh khu nhà mình.

Với người xa lạ, thật khó để có thể xác định được hoạt động trí tuệ mạnh mẽ vốn là đặc trưng hằng ngày của Birkar. Vài năm trước, anh ở Thái Lan, tới thăm gia đình vợ mình. Một buổi chiều, ông của vợ anh hỏi cô, “Chồng cháu làm cái nghề gì vậy? Nó cứ đứng yên trong vườn nhìn chằm chằm lên cây xoài ấy”.

Nhưng với các nhà toán học, Birkar được biết đến nhờ cường độ anh tấn công các vấn đề. “Ấn tượng của tôi là anh ấy có vẻ hơi cô đơn, tập trung và kiên định với các vấn đề mà mình đang nghiên cứu”, Hacon nói. “Anh ấy thực sự yêu thích việc làm chủ những chi tiết kỹ thuật của vấn đề đang nghiên cứu, và đạt thành công lớn”.

Công trình của Birkar về các đa tạp đại số là một phần trong những nỗ lực nghiên cứu lâu nay về cái gọi là chương trình mô hình tối tiểu. Mục tiêu của nó là chứng minh rằng tất cả các đa tạp đại số có thể được giản lược về một trong ba dạng cơ sở thông qua các phép biến đổi song hữu tỷ. Chương trình mô hình tối tiểu đã khởi đầu từ hơn 100 năm trước với các nhà toán học người Ý, những người đầu tiên phân loại các đa tạp đại số hai chiều (các đa tạp đại số ba biến). Gần đây hơn, trong thập niên 1980, Shigefumi Mori đã chứng minh rằng tất cả các đa tạp đại số ba chiều (các đa tạp đại số bốn biến) giản lược về một trong ba dạng này. Mori, nhà toán học ở Đại học Kyoto và hiện là chủ tịch của Hiệp hội Toán học Thế giới, đã được trao Huân chương Fields vào năm 1990 cho công trình này.

Nhưng sau kết quả của Mori, lĩnh vực hình học song hữu tỷ trở nên trầm lặng. “Có những thách thức khổng lồ để mở rộng kết quả này lên các chiều cao hơn”, Birkar nói.

Shokurov là một trong số ít người gặp trở ngại trong lĩnh vực này vào thập niên 1990. Nhờ phần lớn những nỗ lực của ông mà hình học song hữu tỷ đã sống lại vào đầu thập niên 2000. Kể từ đó, các nhà toán học đã tiến những bước lớn trong việc phân loại các đa tạp đại số trong mọi chiều, và Birkar là một trong số nhỏ những nhà toán học ở trung tâm của chương trình này. Năm 2006, cùng với Hacon, James McKernan ở Đại học California, San Diego, và Paolo Cascini ở Đại học Hoàng gia London, anh là đồng tác giả của bài báo khám phá ra cấu trúc phân loại cho các đa tạp dạng tổng quát. Hacon và McKernan sau đó đã được trao giải thưởng Đột phá trị giá 3 triệu USD cho một phần của công trình đó.

Birkar đã có được đóng góp cá nhân lớn lao nhất cho toán học vào năm 2016. Năm đó, anh đã công bố hai bài báo đặt nền móng cho một trong những vấn đề quan trọng nhất liên quan đến bản chất của một số dạng đa tạp Fano cụ thể. Các bài báo đã chứng minh rằng qua những phép biến đổi song hữu tỷ, các đa tạp Fano tạo thành một tập hợp gọn gàng, có thể được định nghĩa bằng một số nhỏ các đặc trưng.

Để hiểu điều này có nghĩa là gì, đầu tiên hãy hình dung về mặt phẳng. Giờ hãy tưởng tượng tất cả các đường thẳng đi qua một điểm trên mặt phẳng. Tồn tại vô hạn các đường thẳng này. Giờ hãy vẽ một hình tròn có tâm là điểm đó. Mỗi đường thẳng kia đều cắt đường tròn ở hai điểm. Bởi thế, mỗi đường thẳng có thể được xác định, hay “tham số hóa” bằng các điểm này (hay chỉ một trong hai điểm này). Thực tế rằng tất cả các đường thẳng có thể được tham số hóa bằng các điểm trên cùng một đối tượng hình học gọn gàng – đường tròn – gợi ra rằng họ các đường thẳng của chúng ta có một trật tự nào đó. Nếu thay vào đó các đường thẳng nằm ngẫu nhiên lung tung trên mặt phẳng, bạn sẽ không thể đưa ra bất cứ khẳng định minh giản nào về chúng.

Trong các bài báo năm 2016, Birkar đã tạo ra một kiểu tham số tương tự cho một số dạng đa tạp Fano cụ thể (những dạng có chiều lẫn lộn với những “kỳ dị nhẹ nhàng”). Anh đã chứng minh rằng, nhờ phép biến đổi song hữu tỷ, các đa tạp Fano trở nên giống như các đường thẳng đi qua một điểm: chúng có quan hệ với nhau đủ trật tự để có thể được tham số bằng một đối tượng hình học gọn gàng. Birkar đã chứng minh rằng tất cả các đa tạp Fano với chiều bất kỳ đều có thể được xác định bằng một số hữu hạn các tham số.

Số vô hạn các đa tạp đại số có thể được xác định bằng một tập hữu hạn các đặc trưng có nghĩa là chúng có chung đặc điểm căn bản nào đó. Nếu bạn tạo ra một phạm trù cho các sinh vật, và bạn cần vô hạn các đặc điểm cho tất cả các động vật trong phạm trù đó, thì phạm trù của bạn sẽ trở nên vô nghĩa. Nhưng nếu bạn có thể dùng một tập hợp hữu hạn các đặc tính để định nghĩa một tập hợp các đối tượng có vẻ như hỗn tạp thì bạn đã tạo ra sự tiến bộ.

“Khi bạn phân loại các thứ với hữu hạn tham số, điều đó có nghĩa rằng chúng chia sẻ rất nhiều tính chất chung”, Birkar nói. “Điều đó giải thích vì sao tính hữu hạn lại quan trọng, bởi vì theo một cách nào đấy thì bạn có thể mô tả điều gì đó về tất cả chúng cùng một lúc”.

Birkar đã chứng minh rằng có một số hữu hạn các đặc trưng xác định các đa tạp Fano, nhưng anh còn muốn biết nhiều hơn thế về họ khổng lồ các phương trình đại số. Khi trở về nhà từ Rio tháng này, anh sẽ có cơ hội khám phá thêm những đặc điểm hình học cụ thể về chúng. Anh sẽ làm điều này với một vị thế mới được khẳng định trong giới toán học và ý thức về sự phi thường khi một người như anh lại có được nó. Cùng lúc đó, anh sẽ vẫn giữ được nguồn động lực theo đuổi toán học từ thuở ban đầu khi anh mới tìm đến lĩnh vực này ở Marivan.

“Bạn có một ý tưởng từ ai đó, nơi nào đó, và bạn tạo ra một thứ mới mẻ”, anh nói. “Bạn đóng góp thứ mới mẻ đó cho cộng đồng và nhờ đó lại tạo ra thêm nhiều thứ đẹp đẽ”.

Hoàng Mai dịch
Nguồn: https://www.quantamagazine.org/caucher-birkar-who-fled-war-and-found-asylum-wins-fields-medal-20180801/