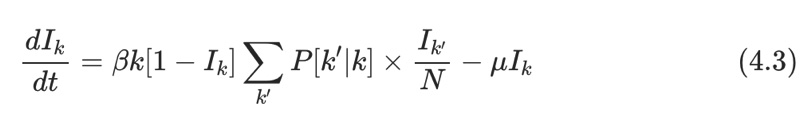Các mô hình phòng ngừa dịch bệnh: Khoa học mạng lưới
Covid-19 không chỉ làm xáo trộn cuộc sống của từng cá nhân mà còn làm thay đổi cách mỗi quốc gia ứng phó với dịch bệnh. Ở khía cạnh này, chúng ta có thể áp dụng thêm một công cụ mới, khoa học mạng lưới để tạo ra các mô hình phòng ngừa dịch bệnh hiệu quả.
Các mô hình lan truyền dịch bệnh từng được Kermack và McKendrick phát triển đầu tiên vào năm 1927 dựa trên lý thuyết trường trung bình động1, các mô hình lan truyền dịch bệnh đầu tiên đã được ứng dụng rộng rãi trong thực tế. Mô hình này dựa trên giả thuyết cơ bản là mỗi cá nhân có thể tương tác với tất cả các cá nhân khác trong xã hội một cách ngẫu nhiên với xác suất giống nhau. Do vậy xác suất bị nhiễm bệnh hay khỏi bệnh của mỗi cá nhân cũng giống nhau và chỉ phụ thuộc vào trạng thái chung của cả xã hội. Bằng cách viết các phương trình cho cá nhân, chúng ta có thể suy rộng ra tỷ lệ trung bình chung cho cả xã hội. Trong phần thứ nhất về khoa học mạng lưới (Tia Sáng số 10/2020), chúng ta đã bàn tới mô hình cổ điển, phần này chúng ta cùng bàn về ứng dụng của khoa học mạng lưới trong việc mô phỏng quá trình lan truyền dịch bệnh.
Mô hình lan truyền cổ điển
Khi áp dụng khoa học mạng lưới để lập các mô hình lan truyền cổ điển, chúng ta đã coi xã hội như một tập hợp N các nhân có thể ở trong một số trạng thái xác định là có khả năng mắc bệnh (Susceptible – ký hiệu S), nhiễm bệnh và có thể lây cho người khác (Infected – ký hiệu I), không còn khả năng mắc bệnh (Removed hay Recovered – đã chữa khỏi và không bị nhiễm lại nữa hoặc đã chết ký hiệu R).
Đây là những yếu tố nền tảng để chúng ta có thể thiết lập nhiều biến thể của mô hình, trong đó hai mô hình phổ biến nhất là SIS (Susceptible-Infected-Susceptible) và SIR (Susceptible-Infected-Removed).
Với mô hình SIS, mỗi cá nhân chỉ có thể có 2 trạng thái là S (khỏe mạnh) hoặc I (nhiễm bệnh) và được khởi đầu ở trạng thái S.
Nếu ở trạng thái S, mỗi cá nhân thì có thể bị nhiễm bệnh và do đó nhanh chóng chuyển sang trạng thái I với xác suất α trong một đơn vị thời gian tỷ lệ. Xác suất này lại tỷ lệ với số người nhiễm bệnh I chia cho tổng số người N,
![]()
Có thể viết lại
![]()
với β là tỷ lệ nhiễm bệnh (infection rate).
Nếu ở trạng thái I, mỗi cá nhân có thể được chữa khỏi và chuyển sang S với xác suất μ trong một đơn vị thời gian, với giả thuyết việc chữa bệnh được áp dụng như nhau cho mọi người bệnh.
Kết hợp lại, chúng ta có thể mô tả quá trình động lực của số nhiễm bệnh (I) và khỏe mạnh (S) bằng các phương trình vi phân (xem 4.1 ở phụ lục) và giải được kết quả (Hình 1). Có thể thấy số bị lây nhiễm (màu nâu) sẽ tăng theo tốc độ hàm mũ trong giai đoạn đầu cho đến khi đạt điểm bão hòa và đi ngang. Khi đó số lượng khỏi bệnh bằng số lượng nhiễm mới và trạng thái cân bằng với số bị nhiễm rất cao.
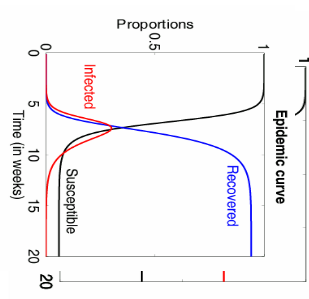
Hình 1: Kết quả giải hệ SIS – nguồn: https://www.cim.pt/
Trong thời gian diễn ra đại dịch, chúng ta còn biết thêm khái niệm R0, hay còn gọi là hệ số lây nhiễm cơ bản và được tính bằng công thức
![]()
có thể hiểu đây là tỷ lệ nhiễm trên tỷ lệ chữa khỏi. Kết quả lan truyền dịch bệnh phụ thuộc vào hệ số R0 như sau: nếu R0>1 thì dịch bệnh sẽ bùng phát (như trong hình trên); nếu R0<1 thì dịch bệnh sẽ tự tiêu biến; nếu R0=1 thì dịch bệnh ở trạng thái dừng đặc hữu (endemic). Để ngăn ngừa dịch bệnh một mặt chúng ta hạn chế lây nhiễm (giảm β), mặt khác tích cực tăng khả năng chữa trị cho người bệnh (tăng μ).
Mô hình phổ biến thứ hai là SIR. Trong mô hình này, một cá nhân từ S có thể bị nhiễm bệnh và chuyển sang I, sau đó cá nhân từ I có thể được chữa khỏi (và không thể lây nhiễm tiếp) hoặc chết đi và chuyển sang R. Cơ chế của mô hình SIR tương tự như SIS, trong đó có thêm trạng thái R (trong SIS thì R ẩn trong S). Kết quả của SIR được giải từ các phương trình vi phân (xem 4.2 ở phụ lục) như sau (Hình 2).
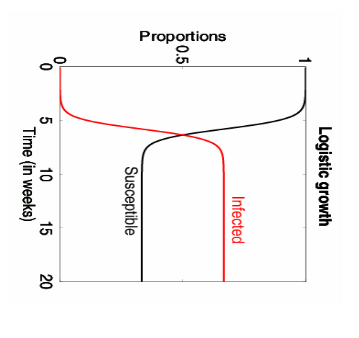
Hình 2: Kết quả giải hệ SIR – nguồn: https://www.cim.pt/
Số lượng bị nhiễm bệnh (màu đỏ) tăng mạnh trong giai đoạn đầu nhưng sau đó đạt đỉnh và đi xuống dần. Số lượng được chữa khỏi tăng tương ứng và bão hòa. Trong giai đoạn cuối, số lượng người khỏe còn quá ít và số lượng bị nhiễm mới giảm theo và tiến gần về 0. (những người chữa khỏi không có khả năng mắc thêm nữa, hoặc đã chết).
Nhìn chung, kết quả từ hai mô hình cổ điển SIS và SIR cho thấy trong giai đoạn đầu, tỷ lệ nhiễm (cho SIS) và chết (cho SIR) sẽ tăng theo hàm mũ và đạt ngưỡng bão hòa sau một thời gian. Ngưỡng này thường sẽ rất cao lên đến nhiều chục % trong dân số nếu không có biện pháp phòng ngừa hiệu quả. Nếu xảy ra tình trạng này thì số lượng người khỏe còn quá ít và số lượng nhiễm rất cao và ổn định vì số lượng nhiễm mới bằng số lượng khỏi (βS=μI). Đây chính là trạng thái miễn dịch cộng đồng.
Mô hình lan truyền theo mạng lưới
Dù các mô hình cổ điển về lan truyền dịch bệnh hiệu quả trong quá khứ nhưng một thế giới mới với những tương tác xã hội ngày một phức tạp và mở rộng đòi hỏi những mô hình mới.
Các giả thuyết cho mỗi cá nhân giống nhau và giao tiếp ngẫu nhiên đều trong toàn xã hội của các mô hình cổ điển còn khá đơn giản. Trên thực tế, mỗi người có mạng lưới tương tác xã hội của riêng mình. Phần lớn các cá nhân chỉ tương tác với một số lượng hạn chế người khác, trong khi đó có một phần nhỏ cá nhân tương tác với rất nhiều người khác. Dựa trên mô hình mạng lưới, Diekmann2 cho rằng, hệ số lây nhiễm cơ bản R0 cần phải điều chỉnh tính đến cấu trúc của mạng lưới tương tác.
Mạng lưới tương tác xã hội cũng giống như nhiều mạng lưới phức hợp khác (complex networks) với nhiều đặc trưng riêng biệt, trong đó các quan trọng nhất về cấu trúc sự phân bố của bậc theo hàm mũ và tính phân nhóm (mạng tương tác xã hội thường phân cụm thành những nhóm riêng biệt. Phần lớn các cá nhân chỉ tương tác với những cá nhân trong cùng một nhóm, một phần nhỏ các cá nhân tương tác với những cá nhân trong nhiều nhóm khác nhau. Các cá nhân này mang tính liên kết rất cao và có thể, nhưng không nhất thiết, là các cá nhân có bậc cao hoặc rất cao) (Hình 3).
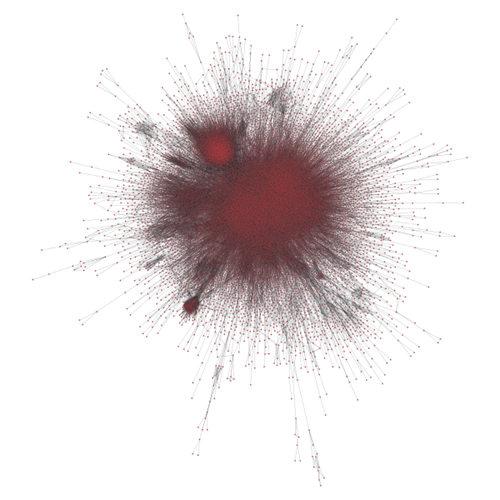
Hình 3: Một mạng lưới xã hội với tính phân nhóm cao – nguồn: [3]
Để mô phỏng cho sự phân bố kết nối khác nhau trong quá trình lan truyền dịch bệnh, Pastor-Satorras và Vespignani (2001) đề xuất4 xét những cá nhân có cùng số bậc tương tác k thì có xác suất nhiễm bệnh giống nhau, còn không thì sẽ khác nhau và tỷ lệ theo số bậc k này. Tiếp đó các tác giả kế thừa trên lý thuyết trường trung bình động cho mỗi giá trị k và phát triển thành mô hình trường trung bình theo bậc (degree-based mean-field theory DBMF). Phương trình vi phân được điều chỉnh lại cho mỗi giá trị bậc k (xem 4.3 ở phụ lục) và có thể giải một cách xấp xỉ bởi phương pháp phân tích trung bình tuyến tính [6] (lời giải chính xác không khả thi). Kết quả chính của mô hình này là điều kiện xảy ra bùng phát dịch (điểm tới hạn) nếu:
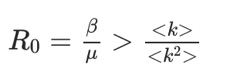
(<> là ký hiệu của kỳ vọng, giả thiết các nút không tương quan (uncorrelated network)).
có nghĩa là hệ số lây nhiễm cơ bản của mạng lưới sẽ bằng tỷ lệ trung bình của bậc và trung bình của bình phương bậc.
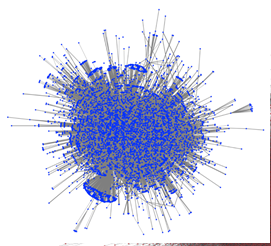
Hình vẽ trên (bên trái) là một ví dụ một mạng xã hội nhỏ gồm 6005 nút với các thông số mạng là:
Giả sử tỷ lệ chữa khỏi μ=0.4 thì xác suất nhiễm bệnh khi tiếp xúc β cần phải dưới giá trị μ
 |
 |
Figure 4+5: Một mạng lưới xã hội với phân bố bậc dạng hàm mũ và tính phân nhóm cao ở trạng thái ban đầu (bên trái) và trạng thái cách ly (hạn chế tương tác/giảm số cạnh – bên phải) nguồn: [3]
Cũng với tỷ lệ chữa khỏi μ=0.4 thì xác suất nhiễm bệnh khi tiếp xúc β cần phải dưới giá trị mới là μ
Bên cạnh phương pháp lấy trung bình theo bậc nói trên, chúng ta có thể mô phỏng trực tiếp quá trình lây lan theo từng đỉnh và cạnh. Phương pháp này đặc biệt có ích nếu tính đến tính phân nhóm và các tính chất đa dạng khác của mạng tương tác xã hội thực tế (mà các mô hình lý thuyết không mô tả hay giải được).
Điểm mạnh của phương pháp mô phỏng trên mạng lưới là chúng ta có thể lường trước được ảnh hưởng của các yếu tố của mạng lưới, ví dụ như tính phân nhóm hay sự phản ứng khác nhau của mỗi cá nhân khi tiếp xúc người bệnh. Đây là các yếu tố thực tế nhưng rất khó đưa vào mô hình giải tích để giải tường minh.
Ngoài ra, với mạng lưới, chúng ta cũng có thể mô phỏng các hành động ngăn ngừa dịch bệnh cụ thể hơn, ví dụ như: ngăn chặn cả một nhóm, ngăn chặn bằng dò đường ngẫu nhiên, ngăn chặn theo cường độ tương tác… Từ đó có thể đưa ra các số liệu hỗ trợ cho các quyết định phòng ngừa nhằm tối ưu hiệu quả của tác động hoặc giảm thiểu chi phí cho một mục tiêu xác định.
Điểm thuận lợi lớn nhất khi chúng ta áp dụng những mô hình này là máy tính và dữ liệu xã hội đều đang sẵn có, do đó các phương pháp mô phỏng trên mạng lưới sẽ càng trở nên có nhiều ưu thế so với các cách tiếp cận truyền thống trong mô phỏng lan truyền bệnh dịch, không chỉ trong Covid-19 mà còn trong tương lai. □
——-
Tham khảo
[1] W. O. Kermack and A. G. McKendrick, Contributions to the mathematical theory of epidemics part I, Proc. R. Soc. Edinb., A115, 700–721, 1927.
[2] Diekmann, O., H. Heesterbeek, and T. Britton (2012), Math- ematical Tools for Understanding Infectious Disease Dynamics (Princeton University Press, Princeton, USA).
[3] Pastor-Satorras, R., and A. Vespignani (2001b), Phys. Rev. Lett. 86, 3200.
[4] Romualdo Pastor-Satorras, Claudio Castellano, Piet Van Mieghem, Alessandro Vespignani, “Epidemic processes in complex networks”. Review of Modern Physics 87(3) 2014
[5] Boguna , M., and R. Pastor-Satorras (2002), Phys. Rev. E 66, 047104.
[6] Bài giới thiệu về các mô hình cổ điển của TS. Hoàng Ngọc Thạch và TS. Phan Thị Hà Dương (VinIF) với các tham số cập nhật cho dịch bệnh Covid-19. (http://vinif.org/vi/khoa-hoc-thuong-thuc/read/1/mo-hinh-du-bao-ngan-han-va-dai-han-kha-nang-lan-rong-cua-dich-2019-ncov-tu-vu-han-o-pham-vi-trung-quoc-va-quoc-te)
Phụ lục
– Phương trình hệ SIS:
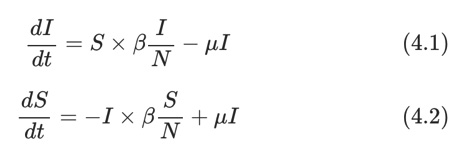
Phương trình mô tả tốc độ nhiễm bệnh cho các nút có bậc k trong mạng lưới: