Chuyện về một dòng họ Toán học hiếm có: Gia đình Bernoulli
Trong lịch sử Toán học, có một dòng họ có sự đóng góp rất lớn, cho nhiều lĩnh vực khác nhau, liên tục trong một thời gian dài, đó là gia đình Bernoulli. Trong hai thế kỷ 17 và 18, gia đình Bernoulli đã mang lại ít nhất là tám nhà Toán học tên tuổi, trong số ấy có ba người có ảnh hưởng nổi trội nhất và định hình nhiều lĩnh vực của toán học trong suốt hai thế kỷ này là Jacob Bernoulli (1654 – 1705), Johann Bernoulli (1667 –1748) và Daniel Bernoulli (1700 – 1782).
LTS: TS. Lê Quang Ánh, một cộng tác viên thân thiết của Tia Sáng với các bài viết về các nhà toán học và lịch sử toán học, mới qua đời tại Mĩ sau một thời gian lâm bệnh nặng. Số báo này, Tia Sáng xin giới thiệu bài viết cuối cùng của ông “Chuyện về một dòng họ toán học hiếm có: Gia đình Bernolli”, như một lời chia tay tới độc giả.
Gia đình Bernoulli

Bức tranh anh em nhà Bernoulli: Jean (Johann) Benoulli (1667-1748) ở bên tay phải và Jacques (Jacob) Bernoulli (1654-1705) ở bên tay trái. Nguồn: sciencephoto.com
Dòng họ Bernoulli có nguồn gốc từ Hà Lan, theo đạo Tin Lành nhánh Calvinism (nhánh Tin Lành Calvinism do John Calvin (1509–1664) thành lập tách khỏi ảnh hưởng của Thiên Chúa giáo La Mã). Năm 1567, vua Philip của Tây Ban Nha đã gửi một đạo quân hùng mạnh đi trừng phạt những xứ nào chống lại vua chúa Tây Ban Nha, chống lại Thiên Chúa giáo La Mã, thiết lập lại uy quyền. Trước sự đe dọa ấy, gia đình Bernoulli chạy trốn qua Basel, Thụy Sĩ, khi ấy Thụy Sĩ là một xứ thương mại giàu có nhất ở Trung Âu. Các thành viên gia tộc Bernoulli đều làm thương mại, và họ mau chóng trở thành những thương gia giàu có. Những nhà Toán học Bernoulli đều xuất phát từ đời Nicolas Bernoulli (1623 – 1708), thương gia thành đạt ở thành phố Basel, Thụy Sĩ. Mặc dù ông Nicolas không có biểu hiện nào về năng khiếu Toán học, nhưng các thế hệ con cháu của ông về sau hầu hết là những nhà Toán học tài năng, trong số đó có những người tầm cỡ hàng đầu châu Âu thời ấy: Jacob Bernoulli, Johann Bernoulli và Daniel Berboulli.
Có thể nói cùng với Isaac Newton, Gottfried Leibniz, Leonhard Euler, và Joseph Lagrange, ba nhà Toán học Bernoulli đã đóng góp, phát triển, định hình các lĩnh vực Tính vi-Tích- phân, Hình học, Cơ học, Nhiệt động học (Thermodynamics), Thủy động học (Hydrodynamics), Quang học, Thiên văn học, Xác suất học trong suốt thế kỷ 17 và 18.
Jacob Bernoulli
Jacob Bernoulli là con trai lớn nhất của Nicolas Bernoulli, được xem như là một trong số những nhà Toán học có ảnh hưởng rất lớn thời bấy giờ mặc dù xuất thân từ một gia đình không có truyền thống Toán học hoặc Khoa học. Cha mẹ buộc ông phải học Triết học và Thần học, những môn không thể thiếu để trở thành một người thượng lưu thành đạt của xã hội thời ấy. Ông tốt nghiệp Thần học năm 1676, sau đó rời bỏ gia đình lên Geneva làm chân giáo viên dạy kèm Toán học và Khoa học để kiếm sống. Một thời gian ngắn sau đó, ông qua Pháp, ở đó trong hai năm theo học Toán với những người theo trường phái Descartes. Năm 1681, ông sang Hà Lan, rồi từ đó tới Anh. Tại London, ông gặp gỡ một số nhà Toán học và Khoa học nổi tiếng trong đó có Robert Hook (1635 – 1703), Robert Boyle (1627 –1691). Ông vẫn giữ mối liên lạc trong nhiều năm sau qua thư tín. Qua những chuyến đi đó đây để học hỏi, ông đã định hướng hẳn cho mình hai lĩnh vực chính, đó là Toán học và Thiên văn học. Năm 1683, ông trở về lại Thụy Sĩ và xin được chân giảng dạy Toán- Cơ tại Đại học Basel, mặc dù gia đình ông phản đối.
Trong khoảng thời gian từ năm 1682 tới 1704, Jacob Bernoulli đã công bố năm tác phẩm về chuỗi số vô tận, trong đó ông đưa ra nhiều kết quả quan trọng. Thí dụ ông chứng minh được chuỗi số điều hòa
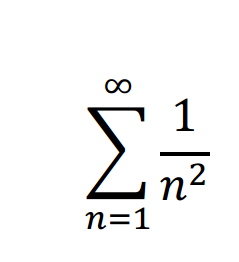
là phân kỳ. Thật ra kết quả này đã được nhà Toán học Ý Pietro Mengoli (1626 – 1686) chứng minh khoảng 40 năm trước. Ngoài ra, Jacob còn chứng minh được chuỗi số
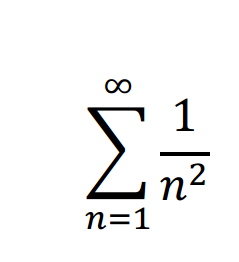
là hội tụ, tuy không tìm được giá trị của tổng số nhưng ông đã chứng minh được tổng số này nhỏ hơn 2. (Khoảng 30 năm sau, năm 1734, Euler đã chứng minh được tổng này bằng π2/6).
Tháng 5 năm 1690, ông cho công bố một bài báo quan trọng về đường đẳng thời (Isochrone hay tautochrone curve)1 trên tờ Acta Eruditorum, tờ báo uy tín được thành lập từ năm 1682 do chính Leibniz làm chủ bút đầu tiên. Jacob Bernoulli chứng minh được bài toán xác định đường đẳng thời tương đương với bài toán giải một phương trình vi phân bậc nhất không tuyến tính. Bài toán này trước đó đã được Christian Huygens (1629 – 1695) vào năm 1659 giải theo hướng Vật lý học. Nhưng chính Jacob Bernoulli là người đầu tiên dùng chữ tích phân (Integral) và các phép tính tích phân để giải bài toán này2. Cũng qua bài báo này, Jacob Bernoulli thiết lập và đưa ra phương pháp giải phương trình vi phân gọi là phương pháp phân ly biến số (method of separation of variables). Đường cong đẳng thời có tên gọi là đường cycloid. Năm 1696, Jacob Bernoulli đưa ra được cách giải phương trình vi phân dạng
y’ = p(x)y + q(x)y’’ ngày nay chúng ta gọi là phương trình Bernoulli. Ông đã áp dụng phương trình này để giải nhiều bài toán Hình học và Cơ học.
Bây giờ ta nói về đường cong có tên là đường dây xích (Catenary theo tiếng Anh hay là Chaînette theo tiếng Pháp). Đó là dạng của đường cong của một dây xích treo giữa hai trụ dưới tác dụng của trọng lượng của nó. Nhà Toán học và Thiên văn học người Ý Galileo Galilei (1564 – 1642) đã nghĩ đến đường cong này và cho rằng đó là một phần của một parabol. Năm 1646, Huygens, khi ấy mới 16 tuổi, đã chứng minh được kết luận của Galileo là sai. Tháng 5 năm 1690, Jacob Bernoulli chính thức đưa bài toán này lên tờ Acta Eruditorum như là một bài toán thách thức: “Hãy xác định hình dạng đường cong của một sợi dây đồng chất (khối lượng phân phối đều) được treo giữa hai điểm cố định.” Một năm sau, trong số báo tháng 6 năm 1691, có ba lời giải được công bố: một của Huygens, một của Leibniz và một của Johann Bernoulli, em trai út của Jacob Bernoulli. Cả ba lời giải đều đi tới cùng kết quả nhưng bằng ba cách hoàn toàn khác nhau. Phương trình Descartes của đường cong ấy là:
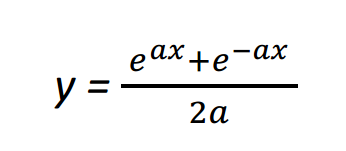
trong đó a là hằng số tùy thuộc vào khối lượng và sức căng của sợi dây. Nghiên cứu về đường dây xích được áp dụng rộng rãi trong xây dựng và kiến trúc.
Jacob Bernoulli là một trong những nhà Toán học tiên phong trong lý thuyết xác suất. Bài báo đầu tiên của ông về xác suất công bố năm 1685. Đóng góp lớn nhất của Jacob Bernoulli là nghiên cứu mang tên Ars Conjectandi (Nghệ thuật suy đoán), tác phẩm này chỉ được công bố năm 1713 sau khi ông mất 6 năm. Trong tác phẩm này Jacob Bernoulli viết về các phép tính hoán vị, tổ hợp, chuỗi vô tận, phân phối nhị thức (binomial distribution), định luật về số lớn (Bernoulli law of large numbers). Ngoài ra, Jacob là người chứng minh được bất đẳng thức Bernoulli thú vị sau đây:
trong đó x là số thực khác 0 và lớn hơn -1.
Cũng chính Jacob Bernoulli là người đầu tiên chứng minh được
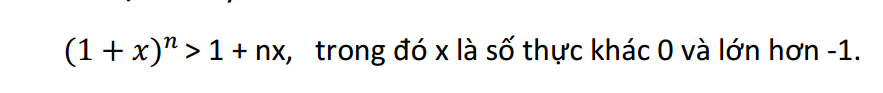
tồn tại và giá trị của giới hạn nằm giữa số 2 và số 3. Sau này nhà toán học Euler (1707-1783) xác định được chính xác đó là số e,
nghĩa là 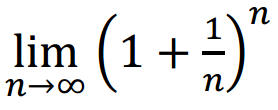 =e.
=e.
Jacob Bernoulli còn quan tâm một cách thích thú đến những đường cong xoắn ốc logarithm mà Descartes đã giới thiệu từ năm 1637.
Jacob Bernoulli giữ ghế trưởng khoa Toán Đại học Basel từ năm 1695 cho đến khi ông qua đời năm 1705. Trên bia mộ của ông ngoài tên tuổi và công trạng, người ta có khắc hình một đường cong xoắn ốc logarithm.
Johann Bernoulli
Johann là em út của Jacob, nhỏ hơn Jacob 13 tuổi và cũng phải học Triết học và Thần học giống anh trai Johann để trở thành những người thượng lưu theo mong muốn của cha. Trong thời gian học Y khoa nhưng không ra hành nghề, Johann nhờ anh Jacob (lúc ấy đã trở thành giáo sư Toán ở Đại học Basel) dạy thêm Toán và chẳng bao lâu có thể tự một mình đọc được các tác phẩm của Leibniz, rồi tự nghiên cứu Toán học, đặc biệt là lý thuyết và kỹ thuật về phép tính vi-tích phân – một ngành Toán hãy còn rất mới mẻ lúc bấy giờ. Jacob mau chóng nhận ra rằng em mình có một năng khiếu Toán rất đặc biệt và mình không có gì phải dạy thêm cho Johann nữa.
Rồi hai anh em hợp tác cùng nghiên cứu một số vấn đề nhưng mối hợp tác ấy mau chóng tan vỡ vì những tranh cãi đôi khi ra ngoài phạm vi Toán học. Cái tôi của cả hai anh em Jacob và Johann quá lớn tới mức cả hai không thể nhân nhượng nhau. Nếu bỏ qua cá tính và những tai tiếng do quan hệ đối xử không tốt với anh trai Jacob, thì Johann là một nhà Toán học xuất sắc. Những gì ông làm được cho Toán học, đặc biệt là trong vi-tích phân còn phong phú hơn cả Jacob. Chính Johann Bernoulli là người dạy Toán cho nhà toán học Euler tại Đại học Basel sau này. Năm 1694 ông nghiên cứu về hàm y = xx Ông nghiên cứu chuỗi số vô tận bằng cách dùng phương pháp tích phân từng phần. Ông cũng đạt được nhiều thành quả trong việc giải phương trình vi phân, khám phá ra các hàm lượng giác hyperbol và những phương trình vi phân để xác định chúng. Vì nhiều thành quả trong nghiên cứu về các phép tính vi-tích phân và phương trình vi phân nên năm 1694 ông được mời làm giáo sư, rồi trưởng khoa ở Đại học Groningen, Hà Lan.

Bên trái là St Louis gateway, bên phải là những vòm trong trường ĐH Oxford. Đó là những hình có dạng catenary úp ngược.
Trở lại bài Toán đường dây xích (catenary) mà Jacob Bernoulli đã đăng trên tờ Acta Eruditorum năm 1690 như là một thách đố. Johann dùng ngay phương pháp vi tích phân của Leibniz để giải bài toán, lời giải của Johann tỏ ra vượt trội hơn lời giải của Huygens và lời giải của chính Leibniz. Bài toán đường đoản thời (brachistochrone curve)3 cho thấy tài năng và cá tính kênh kiệu của Johann Bernoulli. Trong số báo Acta Eruditorum tháng 6 năm 1696, Johann đăng thông báo sau đây: Tôi, Johann Bernoulli, gửi những lời này tới những nhà Toán học xuất sắc nhất thế giới. Không có gì thu hút những con người thông minh bằng bài toán thử thách mà lời giải của họ sẽ làm cho họ nổi tiếng và lưu danh lại cho đời sau. Tôi hy vọng sẽ thu hút được sự chú ý của giới Khoa học, trong đó có những nhà Toán học giỏi nhất của thời đại chúng ta như là Pascal và Fermat của thế hệ trước. Bài toán của tôi sẽ cho họ thể hiện phương pháp và tài năng của họ. Nếu họ gửi lời giải tới tôi, tôi sẽ đánh giá và công bố sự xứng đáng của họ.
Và đây là bài toán của Johann Bernoulli:
Cho hai điểm A và B nằm trong mặt phẳng thẳng đứng P (A cao hơn B). Hãy xác định đường nối hai điểm A và B và nằm trong mặt phẳng P sao cho một điểm chỉ chịu trọng lực chạy từ A đến B trong thời gian ngắn nhất.
Có 5 bài giải đúng được gửi tới, trong đó 4 bài giải từ những nhà Toán học đã thành danh: De L’Hôpital, Leibniz, Jacob Bernoulli và chính của Johann Bernoulli. Còn bài giải thứ năm của một người ghi là vô danh. Bài giải của người vô danh này được Johann ghi bên lề là “Ex ungue Leonem” (Nhận biết con sư tử qua móng vuốt của nó)4. Qua cách viết, qua lập luận và tính toán, Johann đã nhận ra được lời giải này của Newton và sau này Newton cũng công nhận như vậy. Newton còn nói thêm rằng ông đã mất 12 tiếng đồng hồ để giải bài toán ấy. Lời giải cho bài Toán này là một phần đường cycloid lật ngược.
Phương pháp giải bài toán đường đoản thời của Johann Bernoulli rất độc đáo. Nó làm cách mạng phép tính vi-tích phân của Leibniz để trở thành một phép tính mới: phép tính biến phân (Calculus of variations).
Một câu chuyện nổi tiếng không kém là chuyện giữa Johann Bernoulli và nhà Toán học Guillaume de L’Hôpital (1661 – 1704). Ta nên nhớ rằng de L’Hôpital lớn hơn Johann 6 tuổi và đã có tên tuổi trong giới Toán học rồi. Khoảng giữa năm 1694, khi chưa có nghề nghiệp gì, Johann đến Paris – trái với ý kiến của cha mẹ ông – để làm gia sư cho một thanh niên quý tộc người Pháp, đó là Hầu tước Guillaume de L’Hôpital. Johann dạy Hầu tước phép tính vi-tích phân của Leibniz, nhưng vì cần tiền cho nên khi rời khỏi Paris ông vẫn gửi bài tới cho Hầu tước theo yêu cầu của ông này, để tiếp tục được trả lương. Năm 1695, Johann Bernoulli gửi tới Hầu tước de L’Hôpital qui tắc nói rằng nếu hai hàm số có đạo hàm và cả hai bằng 0 tại cùng một điểm, và nếu giới hạn tỷ số hai đạo hàm ấy tồn tại tại điểm ấy, thì giới hạn của tỷ số hai hàm số bằng giới hạn tỷ số hai đạo hàm tại điểm ấy. Diễn tả qui tắc ấy thành công thức như sau:
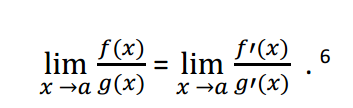
Qui tắc này có trong phép tính vi-tích phân mà mọi sinh viên đều biết dưới tên gọi là qui tắc L’Hôpital. Hầu tước de L’Hôpital, với sự thỏa thuận của Johann Bernoulli, công bố qui tắc này trong cuốn sách của ông mang tên Analyse des Infiniment Petits pour l’Intelligence des Lignes Courbes (Giải tích các vô cùng nhỏ để hiểu các đường cong) xuất bản năm 1696 mà không đề cập tới ai đã phát minh ra qui tắc này. Tuy nhiên trong lời nói đầu, de L’Hôpital có viết lời cảm ơn gửi tới Johann Bernoulli và Leibniz về một số kết quả có trong sách.
Johann Bernoulli có tham dự vào cuộc tranh cãi giữa Newton và Leibniz về vấn đề ai là người đầu tiên phát minh ra phép tính vi-tích phân. Trong cuộc tranh cãi này hai anh em Jacob và Johann Bernoulli hoàn toàn ủng hộ Leibniz, nhất là Johann ủng hộ nhiệt tình, phản bác tích cực cáo buộc cho rằng Leibniz đạo ý tưởng của Newton do hầu hết những nhà Toán học đương thời của Anh đưa ra. Chính bài toán đường đoản thời mà Johann thách đố có dụng ý cho thấy ưu thế của phép tính vi-tích phân khai triển theo cách của Leibniz so với phương pháp vi-tích phân khai triển từ khái niệm chuyển động (fluxion: vận tốc) theo cách của Newton. Ngoại trừ người vô danh lúc ấy (tức là Newton), không có một người nào theo phương pháp của Newton giải được bài toán ấy. Điều này không những xác nhận ưu thế của phép tính vi-tích phân của Leibniz mà còn cho thấy Leibniz là người sáng lập ra phép tính vi-tích phân một cách hoàn toàn độc lập với Newton.
Daniel Bernoulli
Johann Bernoulli có ba người con trai, thứ tự từ lớn đến nhỏ là Nicolas II (1687 – 1759), Daniel (1700 – 1782) và Johann II (1710 – 1790). Cả ba đều là những nhà Toán học có tiếng thời ấy, nhưng Daniel xuất sắc hơn cả. Là một nhà Toán học xuất sắc và nổi tiếng nhưng Johann Bernoulli không muốn các con theo con đường của mình. Ông hướng các con vào con đường thương mại với lời giải thích là “Toán không thể nào đem lại sự giàu có”. Nhưng cả ba người con là Nicolas II, Daniel và Johann II đều chống lại ý cha. Daniel thỏa thuận với cha chọn con đường như cha mình: học Y khoa, nhưng rồi cũng như cha, Daniel không hành nghề Y. Ông tự học Toán, học Vật lý, học qua trao đổi và tranh luận với nhiều nhà Khoa học ở Ý, Đức và Pháp.
Năm 1724, khi đang ở Venice, Ý, Daniel xuất bản cuốn Exercitationes Quaedam Mathematicae (Bài tập Toán học). Đây là tập hợp về một số vấn đề Toán áp dụng vào Vật lý. Qua ấn phẩm này, người ta thấy tài năng áp dụng Toán học vào Vật lý của Daniel bắt đầu xuất hiện. Năm 1733 ông hoàn thành cuốn Hydrodynamica (Thủy động học) nhưng đến 5 năm sau, tức là 1738, cuốn sách mới được xuất bản. Tác phẩm này thời ấy được xem như nền tảng cho bộ môn mới mẻ này.

Daniel Bernoulli (1700 – 1782).
Từ 1725 đến 1757, ông giành tổng cộng 10 giải thưởng của Viện Hàn lâm Khoa học Paris, hầu hết các đề tài đều liên qua đến Toán học áp dụng vào Thiên văn, vào Thủy động học, vào Hải hành trên biển, vào Từ học. Năm 1734 Daniel và cha của mình – nhà Toán học Johann Bernoulli – cùng được giải thưởng của Hàn lâm Viện Khoa học Paris. Giải thưởng năm 1740 Daniel chia cùng với Euler và Mac Laurin trên đề tài dùng lý thuyết của Newton để nghiên cứu về thủy triều do sức hút của Mặt trăng và Mặt trời.
Sau khi cuốn Exercitationes Quaedam Mathematicae được xuất bản, tài năng của Daniel được giới Khoa học cả châu Âu biết tới. Năm 1725, theo lời giới thiệu của Leibniz, nữ hoàng Catherine I của Nga mời Daniel và người anh trai là Nicolas II (1695 – 1726) sang Nga tổ chức và điều hành ngành Toán của Hàn lâm Viện Hoàng gia Saint-Petersburg mới được thành lập. Vừa mới hơn một năm, Nicolas II chết vì bệnh lao. Sau đó, một ngôi sao đang lên còn rất trẻ (mới 20 tuổi) là bạn thân của hai anh em nhà Bernoulli và là học trò xuất sắc nhất của Johann Bernoulli tên là Leonhard Euler (1707 – 1783) sang thay thế vị trí của Nicolas II.
Còn người em Daniel Bernoulli đã được lưu danh rất nhiều trong các vấn đề Toán học áp dụng vào Vật lý: Động học chất khí (kinetic theory of gases), hiệu ứng Bernoulli trong cơ học lưu chất, hiệu ứng này sau này được áp dụng trong kỹ thuật hàng không. Lĩnh vực nổi tiếng nhất của ông là góp phần phát triển lý thuyết về bộ môn xác suất. Năm 1731, ở Saint – Petersburg, ông cho xuất bản cuốn Specimen Theoriae Novae de Mensura Sortis (Lý thuyết mới về tính toán các vận may rủi). Đây là tác phẩm nghiên cứu về xác suất trong đó Daniel có đề cập tới vấn đề số hy vọng (expected values) và cùng với người anh là Nicolas II đưa ra một bài toán sau này nổi tiếng với tên gọi nghịch lý Saint-Petersburg.
Trong những năm cuối đời, Daniel tiếp tục nghiên cứu về phép tính vi-tích phân, cơ học, và nhiều vấn đề áp dụng Toán học vào Vật lý. Ông là thành viên của nhiều Hàn lâm Viện Khoa học: Hàn lâm Viện Paris, Hàn lâm Viện Hoàng gia Anh, Hàn lâm Viện Berlin, Hàn Lâm Viện Saint-Petersburg. □
——
Chú thích:
1. Đường đẳng thời là đường cong đi xuống, trên đó mọi chất điểm chỉ dưới tác dụng của trọng lực, bất kỳ khởi hành ở điểm nào, cũng sẽ đạt điểm đáy trong cùng một thời gian như nhau (đẳng thời= thời gian bằng nhau)
2. Leibniz dùng chữ calculus summatorium để chỉ tích phân.
3. Đoản thời = thời gian ngắn.
4. Thì ra Johann cũng còn biết nể nang con sư tử của nước Anh!
