Emmy Noether và vấn đề bảo toàn năng lượng
Năm nay vừa đúng 100 năm từ năm 1918 Noether (23/3/1882 – 14/4/1935) công bố công trình “Invariante Variationsprobleme - Các bài toán biến phân bất biến”. Năm này, Noether vừa tròn 36 tuổi.

Trên hình vẽ là con đường Đại học Erlangen,năm 1916. Emmy Noether (23/3/1882-14/4/1935) đã sinh ra trong thành phố này và ở đây đến năm 1925 và rời thành phố để đến Gottinger theo lời mời của David Hilbert và Felix Klein.
Công trình với các định lý Noether hiện nay được xem là một cột mốc quan trọng trong sự phát triển của vật lý hiện đại thế kỷ 20.
Cũng nói thêm, công trình chỉ nổi tiếng sau Noether đã mất.
Điều lý thú đối với các nhà vật lý là tên tuổi Noether lại gắn liền đến một vấn đề lớn trong vật lý là vấn đề bảo toàn năng lượng trong GR (General Relativity – Lý thuyết tương đối tổng quát).
Emmy Noether chứng minh hai định lý quan trọng liên quan đến đối xứng và các định luật bảo toàn.
Định lý thứ I liên quan đến những nhóm biến đổi chỉ phụ thuộc vào một số hữu hạn thông số (ví dụ nhóm quay trong mặt phẳng chỉ phụ thuộc vào một thông số là góc quay), xem tài liệu1.
Định lý thứ II liên quan đến một số hữu hạn các hàm số và đạo hàm của hàm số.
Noether gọi nhóm thứ nhất là “nhóm liên tục hữu hạn” còn nhóm thứ II là các “nhóm liên tục vô hạn”. Hai định lý đó được mang tên là các định lý Noether.
Các định lý được hoàn thành sau khi Hilbert tìm ra nguyên lý biến phân (variational principle) và ứng dụng vào lý thuyết tương đối tổng quát.
Định lý II Noether và vấn đề bảo toàn năng lượng trong GR
Hiện tượng không tìm ra biểu thức mô tả bảo toàn năng lượng định xứ (local) trong GR vào thời bấy giờ đã làm đau đầu những bộ óc vĩ đại như David Hilbert, Felix Klein và thậm chí Albert Einstein.
Các định lý của Noether đã giải quyết được vấn đề đó!
Emmy Noether công bố công trình dưới tiêu đề “Invariante Varlationsprobleme” (viết tắt là I.V.) Hai định lý trong công trình này bộc lộ được mối quan hệ giữa đối xứng và các định luật bảo toàn trong vật lý.
Lúc bấy giờ, Hilbert, Felix Klein đang quan tâm đến việc hoàn thiện GR (General Relativity). Một vấn đề quan trọng là bảo toàn năng lượng trong GR.
Trong GR, năng lượng không được bảo toàn một cách định xứ như trong các lý thuyết trường cổ điển khác (hấp dẫn Newton, điện từ, thủy động học…). Vấn đề bảo toàn năng lượng trong GR đã được nghiên cứu trong nhiều thập kỷ.

Emmy Noether.
Trong ngôn ngữ hiện đại GR là một trường chuẩn (gauge). Nhóm đối xứng của lý thuyết là một nhóm chuẩn. Đây là nhóm biến đổi tọa độ tổng quát (group of general coordinate transformations) có một số vô hạn liên tục các vi tử (generator) vi phân độc lập với nhau. Noether gọi nhóm đó là nhóm liên tục vô hạn (an infinite continuous group). Nhóm Poincare là nhóm con của nhóm này có 7 vi tử vi phân độc lập với nhau. Noether gọi những nhóm như thế là nhóm liên tục hữu hạn (finite continuous group).
Sự khác nhau giữa hai nhóm đó cũng là sự khác nhau giữa 2 định lý của Noether trong công trình I.V.
Định lý I được áp dụng khi ta có nhóm đối xứng liên tục hữu hạn.
Định lý II được áp dụng khi ta có nhóm đối xứng liên tục vô hạn.
Về mặt vật lý trong trường hợp thứ nhất ta có một mật độ năng lượng bảo toàn định xứ. Lúc này tensor năng – xung lượng có div = 0 (divergence free).
Trong trường hợp thứ hai (GR) không có ý nghĩa khi nói đến sự định xứ của năng lượng (definite localization of energy).
Ta cũng có thể thành lập một đại lượng với div = 0 (divergence free) như tensor năng xung lượng như trong SR (Special relativity), song tensor này trong GR lại phụ thuộc vào điều kiện chuẩn (gauge) có nghĩa là không hiệp biến (covariant) dưới các biến đổi tọa độ. Như vậy nếu lấy tensor này dù là có div = 0 thì cũng không có nghĩa là ta có một định luật bảo toàn năng lượng định xứ.
Trong GR biểu thức bảo toàn năng lượng sẽ có một dạng khác. Vì lý thuyết là chuẩn nên ta có nhóm đối xứng liên tục vô hạn mà dịch chuyển thời gian (time translation) là nhóm con.
Định lý II Noether hàm ẩn con đường dẫn đến phương pháp tìm đại lượng gọi là giả tensor (pseudotensor-tiền tố pseudo có nghĩa là “giả”, đại lượng này được gọi như thế vì không hiệp biến dưới các biến đối tọa độ tổng quát).
Một giả tensor lại hiệp biến với các biến đổi tuyến tính của nhóm Poincare và có thể dùng cho các vùng không – thời gian xa các nguồn hấp dẫn để suy ra nguyên lý bảo toàn năng lượng.
Định lý I Noether: ƌνTμν = 0 Khi tác động (action) bất biến đối với dịch chuyển không thời gian thì divergence
Điều này dẫn đến bảo toàn năng lượng định xứ.
Định lý I và cuộc đời của Noether được trình bày đầy đủ trong bài viết lý thú gây nhiều cảm xúc của tác giả Nguyễn Xuân Xanh3 và theo gợi ý của NXX chúng tôi viết bài này nhằm cung cấp thêm một số thông tin về định lý II của Noether.
Song nếu chuyển sang GR thì metric tensor gμν phụ thuộc vào không thời gian. Ta có phương trình Rμν -1/2Rgμν = xTμν
Tensor Tμν mô tả đóng góp của điện từ và các trương vật chất khác song không có đóng góp của hấp dẫn. Vậy T00 không phải là năng lượng toàn phần. Vậy tensor đó không có div = 0. Điều này Hilbert đã hiểu từ năm 1915 song vấn đề chưa hiểu được là làm thế nào mà xác định được nguyên lý bảo toàn năng lượng trong GR.
Hãy đi sâu hơn vào định lý II của Noether.
Định lý II Noether:
Nếu hàm tác động (action) S bất biến đối với nhóm G∞ρ thì tồn tại ρ hệ thức
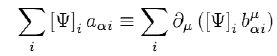
Như vậy định lý II nói rằng có những “đẳng thức phụ thuộc” (dependencies – từ của Noether) giữa các biểu thức Lagrange [Ψ] và các đạo hàm của chúng.
Nhóm G∞ρ = nhóm biến đổi vô hạn chiều phụ thuộc vào ρ hàm bất kỳ, ρ∞ (xμ) , (α = 1,2… ρ) và các đạo hàm bậc một của chúng và cuối cùng là:
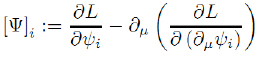
[Ψ]i = 0 là các phương trình Euler – Lagrange cho [Ψ].
Ở đây ta thấy phương trình liên tục dòng có thể suy ra từ đối xứng chuẩn định xứ nhờ Định lý II Noether
Theo định lý II thì phương trình liên tục lẽ dĩ nhiên cũng có thể suy từ các phương trình trường song định lý II cho ta thấy rằng các phương trình trường chỉ là điều kiện đủ (sufficient) mà không là những điều kiện cần (necessary). Điều này trái với trường hợp đối xứng toàn bộ (global) ở đấy phương trình liên tục phải là hệ quả của các phương trình trường xuyên qua định lý I. Ở đấy các phương trình trường vùa là cần và đủ để suy ra phương trình liên tục.
Có thể nói phát biểu gọn hơn.
Định lý II Noether: Tồn tại một số “đẳng thức phụ thuộc” (gọi là dependencies) giữa các hàm Lagrange và các đạo hàm. (derivatives). Những đẳng thức đó trong GR là những đẳng thức Bianchi.
Dependencies = đẳng thức phụ thuộc giữa các trường không xác định bới các phương trình chuyển động.
Theo tài liệu 1 trang 234 định lý II Noether (với các dependencies) đã mở ra “con đường hoàng gia” (royal road) để tiếp cận vấn đề bảo toàn năng lượng trong GR.
Giả tensor (pseudotensor) năng xung lượng trong GR
Trên con đường hoàng gia đó, nhiều nhà vật lý (Jackiw, Weinberg) đã tìm ra một đại lượng quan trọng là giả tensor (pseudotensor-tiền tố pseudo có nghĩa là giả) với div = 0.
T μν eff = T μν + t μν
Ngoài ra Landau &Lifshitz cũng tìm ra được giả tensor theo cách riêng (xem7, Landau & Lifshitz trang 360,…).
Nếu phân tích sâu quá trình tính toán pseudotensor trong7 ta nhận thấy rằng Landau & Lifshitz đã sử dụng hệ thức Bianchi (dùng công thức (92,1) trang 334) nghĩa là đã sử dụng Theorem II Noether.
Pseudotensor này thỏa mãn điều kiện div = 0, và biểu diễn luật bảo toàn năng lượng trong GR 7, trang 361: T μν eff , μ = 0
Các đại lượng t μν phụ thuộc chuẩn, không biến đổi như tensor cho nên được gọi là giả tensor (pseudotensor). Các đại lượng này phụ thuộc các ký hiệu Christofell (xem 7 trang 380).
Sử dụng pseudotensor đó người ta có thể phát biểu một nguyên lý cho việc bảo toàn năng lượng bằng cách lấy tích phân trên một siêu mặt đồng dạng không gian rộng và tiệm cận phẳng.
Và từ đó chúng ta có được một 4-vector Pα năng xung lượng mang cả năng – xung lượng của bức xạ hấp dẫn và là constant theo thời gian.
Vector này hành xử giống như trong SR đối với các biến đổi Lorentz và không phụ thuộc vào tọa độ sử dụng.
Kết luận
Hai định lý quan trọng của Noether là một đóng góp lớn cho vật lý hiện đại. Định lý thứ II đã giúp giải quyết vấn đề bảo toàn năng lượng trong GR, một vấn đề mà những nhà toán học và vật lý, những bộ óc vĩ đại như David Hilbert, Felix Klein và thậm chí Albert Einstein đều phát biểu là một bài toán khó, họ đều khen ngợi Emmy Noether vì thành công này.
——-
TÀI LIỆU THAM KHẢO
1 Dwight E.Neuenschwander,Emmy Noether’s wonderful theorem, Johs Hopkins University Press, Baltimore
2 Katherine Brading and
Harvey R. Brown Noether’s Theorems and Gauge Symmetries
arXiv:hep-th/0009058v1 8 Sep 2000
3 Nguyễn Xuân Xanh, Emmy Noether, Tạp chí Tia Sáng số 19-05.10.2018.
4 DAVID E. ROWE,
Emmy Noether le centenaire d’un théorème, Pour la Science tháng 9/2018Science No 490, tháng 8/2018
5 Nina Byer, E. Noether’s Discovery of the Deep Connection Between Symmetries and Conservation Laws
THE HERITAGE OF EMMY NOETHER IN ALGEBRA, GEOMETRY, AND PHYSICS
http://cwp.library.ucla.edu/articles/noether.asg/noether.htm
6 Hans Ohanian &Remo Ruffini,Gravitation and spacetime
W.WNorton and Company.New York *London,1994,page 358
7 Л .Д Ландау & Е .М Лифшиц
ТЕОРИЯ ПОЛЯ, НАУКА 1973
