Hệ phức hợp: Những biểu hiện đa dạng trong một thế giới phức tạp
Cuối thế kỷ trước, Stephen Hawking đã từng nói rằng thế kỷ 21 sẽ là thế kỷ của hệ phức hợp. Lời tiên đoán của ông đã bắt đầu trở thành hiện thực khi giải Nobel Vật lý năm 2021 là một khởi đầu cho lời tiên nghiệm đó.

Giáo sư Giorgio Parisi. Nguồn: science.thewire.in.
Hệ phức hợp là một hệ thống gồm rất nhiều phần tử tương tác với nhau. Tính chất chung của cả hệ có thể rất khác biệt và không thể suy ra được từ việc nghiên cứu các thành phần riêng lẻ của nó. Ví dụ như hệ có tính chất tự tổ chức (self-organized), tính đột sinh (emergence), khả năng biến đổi tiến hóa (adapt) trong môi trường. Phần lớn các tương tác giữa các phần tử trong hệ thống là phi tuyến tính.
Có thể kể đến các hệ phức hợp như hệ sinh thái hay hệ biến đổi thời tiết, một nền kinh tế hay một mạng xã hội, các mạng truyền tải điện và mạng giao thông. Trong sinh học, các hệ miễn dịch trong cơ thể, bộ não sinh học, một đàn kiến đông, virus lan truyền trong xã hội, cũng có thể coi là hệ phức hợp…1
Chúng ta có thể thấy được phần nào sự đa dạng của các hệ thống đó qua những nghiên cứu của giáo sư Giorgio Parisi của Sapienza ở Rome, Italy, một trong ba nhà khoa học được trao giải Nobel trong năm nay. Ông khởi đầu là một nhà Vật lý lý thuyết, sau đó nghiên cứu về Vật lý thống kê, lý thuyết trường, hệ động lực, vật lý toán, vật lý các hệ đậm đặc.
Các hệ không trật tự kiểu thủy tinh spin
Một trong những phát minh nổi tiếng nhất của giáo sư Parisi là khái niệm thủy tinh spin (“spin-glass”), một tập hợp các mô hình vật lý thống kê có nhiều ứng dụng trong lý thuyết tối ưu, sinh học và y khoa. Từ trường spin là một đặc tính của các hạt cơ bản. Ví dụ ở trong nam châm hàng tỷ tỷ các electron của nguyên tử sắt có spin hướng theo cùng một hướng (lên hoặc xuống) tạo nên một từ trường lớn của miếng nam châm phát ra bên ngoài, gọi là vật liệu từ tính. Phần lớn vật chất trong tự nhiên không có từ tính bởi các electron nguyên tử thường có spin xoay ngẫu nhiên và tổng thể từ trường sẽ bằng 0. Cụm từ “glass” được lấy do có sự tương đồng với các thủy tinh hóa học hay còn gọi là chất vô định hình với các liên kết nguyên tử đặc biệt bất định.
Khái niệm thủy tinh spin kết hợp tính từ tính và tính bất định cho một hệ phức hợp. Một ví dụ của thủy tinh spin là một hợp kim gồm các nguyên tử sắt có từ tính được đặt ngẫu nhiên trong một mạng lưới đều các nguyên tử đồng (hình 1). Mỗi nguyên tử sắt như một nam châm với chiều bị ảnh hưởng bởi các nam châm lân cận. Tuy nhiên làm sao tập hợp các nguyên tử sắt này xoay hướng từ trường một cách tối ưu trong hợp kim?
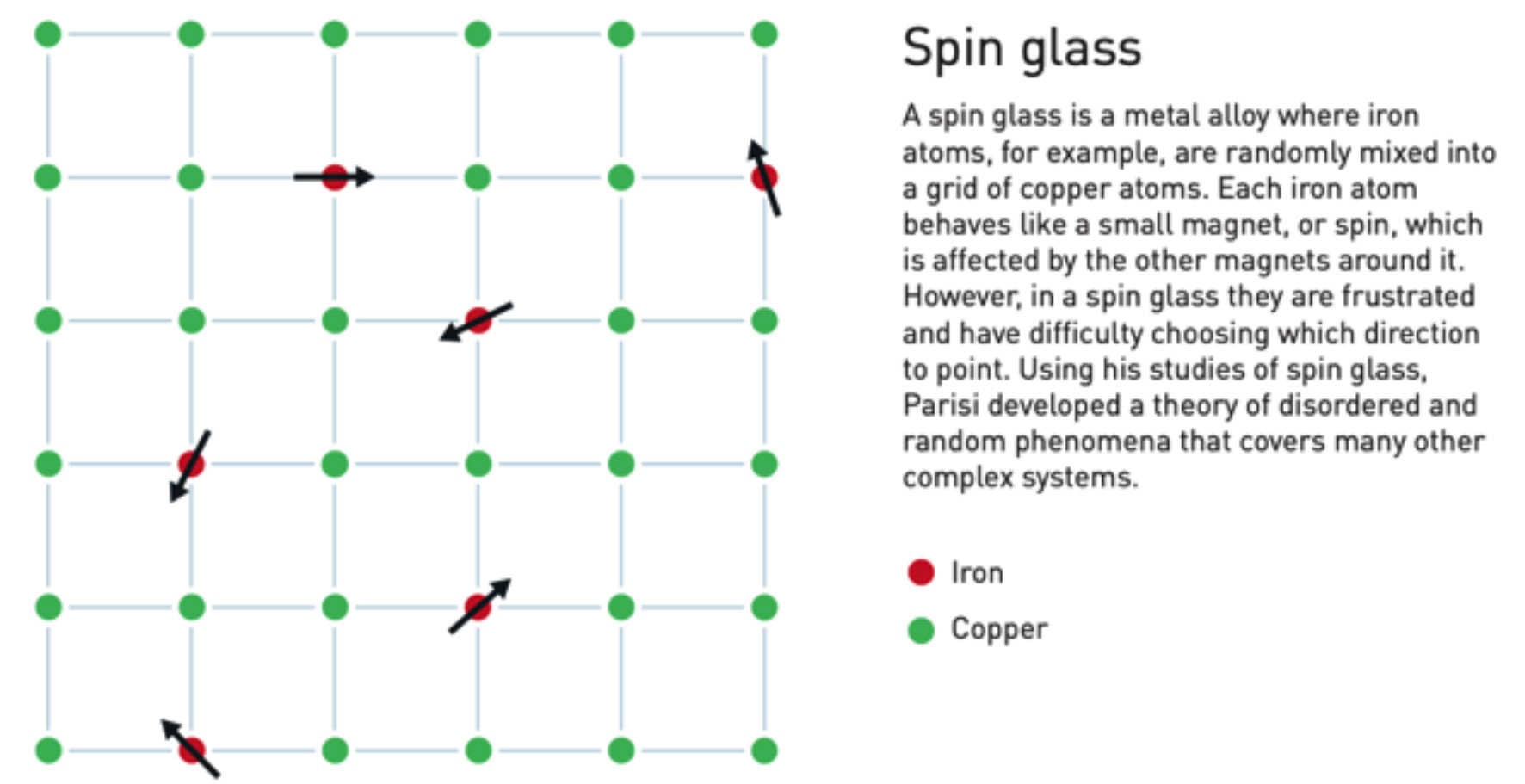
Hình 1: biểu diễn của một hệ thủy tính spin trong hợp kim đồng – sắt.
Câu trả lời sẽ rất khó nếu giả sử các nam châm (nguyên tử sắt) gần nhau đẩy lẫn nhau, tức là buộc chúng phải có chiều nam châm ngược nhau (phản từ tính hay “antiferromagnetic”). Chỉ cần giả sử chúng ta có ba nam châm thì điều này cũng không thể thỏa mãn cho mỗi cặp nam châm như trong hình2. Nếu nam châm A hướng lên, nam châm B hướng xuống thì cặp tương tác AB thỏa mãn điều kiện ngược nhau, nhưng nam châm C dù hướng theo chiều nào cũng không thể thỏa mãn cũng lúc cặp CA và CB. Chúng ta gọi đây là một trạng thái “rối loạn”.
Edwards và Anderson [1] đã rất tài tình giải các hệ thống này với kỹ thuật sao chép (“replica method”) các hàm phân bố và tổng hợp chúng lại dựa trên các lý thuyết trường trung bình (“mean-field”). Tuy nhiên khi giải cho các hệ vô hạn chiều thì kỹ thuật này dẫn đến trạng thái entropy âm, điều này dẫn đến sự đối xứng của kỹ thuật sao chép bị phá vỡ (“broken replica symmetry”) (Blandin [2], and by Bray and Moore [3]).
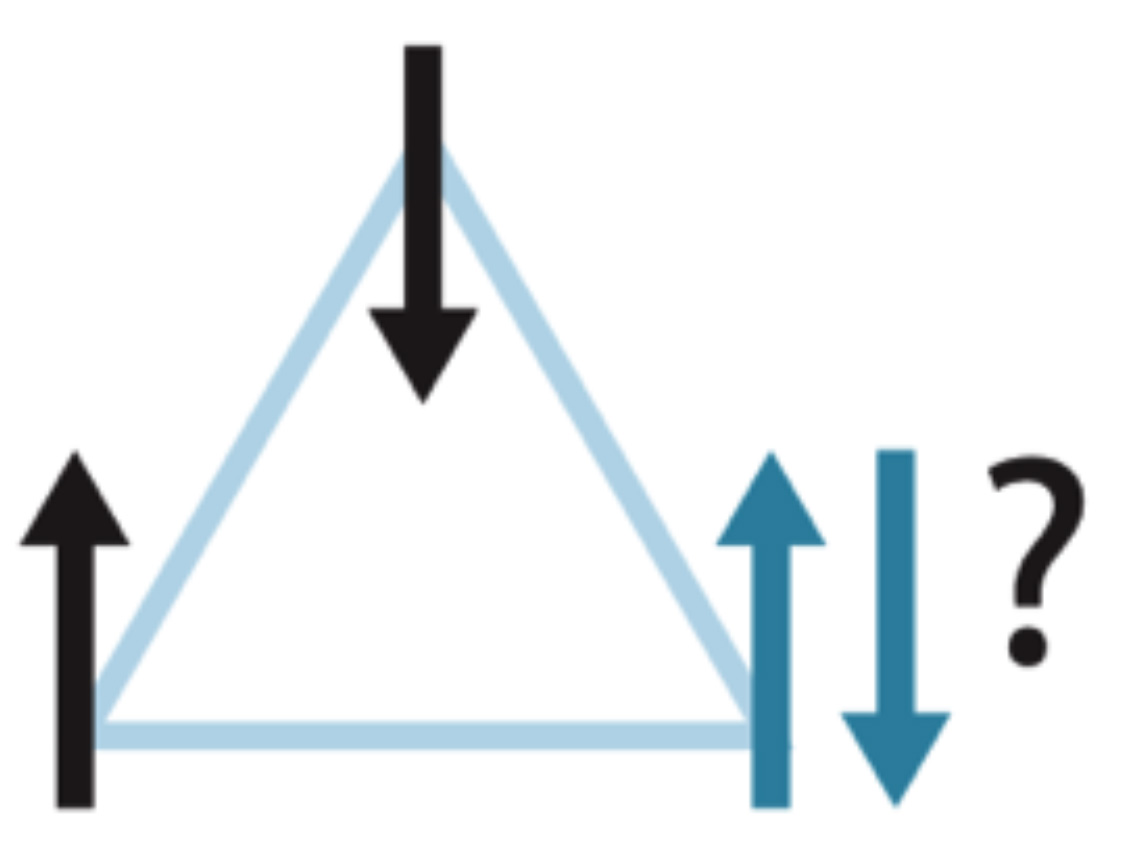
Hình 2: Sự rối loạn: khi một spin hướng lên và một spin hướng xuống thì một spin thứ 3 không thể thỏa mãn cả hai. Làm thế nào để tạo ra một sự cân bằng tối ư? GS. Parisi là bậc thầy của lời giải cho các hệ như vậy.
Giáo sư Parisi đã giải quyết mâu thuẫn này bằng cách chỉ ra rằng ở các trạng thái ổn định, hệ “spin glass” cần có vô hạn các tham số bậc [4, 5]. Đồng thời, ông cũng đưa ra công thức để tính thông số tương quan giữa các bản sao replica của hệ. Điều đó có nghĩa là mặc dù chúng ta có thể không dự đoán chính xác trạng thái của một hệ thủy tinh spin, nhưng chúng ta có được một lý thuyết về tính tương quan giữa các trạng thái có thể có của hệ. Các trạng thái có thể có này co cụm trong không gian N chiều.
Các lý thuyết giải thích hệ thủy tinh spin nhanh chóng được áp đụng cho các hệ tương tự. Ví dụ với mạng neuron của John Hopfield [6], các bản ghi nhớ trong mạng tương ứng với các trạng thái cân bằng khác nhau của hệ thủy tinh spin. Các lý thuyết của hệ thủy tinh spin cũng giúp giải quyết các bài toán tối ưu cổ điển như bài toán tìm đường đi tối ưu cho người bán hàng,…
Một ví dụ thú vị khác của các hệ không trật tự kiểu spin glasss là một bài toán trong khoa học xã hội. Có thể hiểu đơn giản bằng ví dụ của một “hệ xã hội nhỏ” sau: trong một bữa tiệc Alice muốn nói chuyện với Bob, Bob muốn nói chuyện với Charlie nhưng Alice lại không thích gặp Charlie. Có một sự rối loạn ở đây và nếu tưởng tượng là có 100 người với nhiều chục cặp “không thích” như vậy, kết quả sẽ không thể đoán được.

Hình 3: GS. Parisi nghiên cứu sự tạo thành hình dạng đột phát của bầy chim sáo.
Các lý thuyết về hệ thủy tinh spin của giáo sư Parisi có thể áp dụng cho ví dụ trên. Lý thuyết cho thấy cả Alice, Bob, Charlie và những người khách khác sẽ thường xuyên tìm gặp các đối tác khác, kỳ vọng sẽ tạo thành nhóm trò chuyện hợp nhau lớn hơn. Nhưng nếu số lượng người đủ lớn thì sẽ không bao giờ tìm được giải pháp tối ưu mà sẽ có từng nhóm nhỏ trò chuyện – gọi là những giải pháp dưới tối ưu hay (hay các cực trị địa phương). Hệ phức hợp có thể ở trong trạng thái dưới tối ưu nhưng ổn định này trong một thời gian rất lâu (gọi các trạng thái “metastable”). Nhưng chúng cũng biến đổi theo thời gian, đi ra khỏi cực trị địa phương rồi lại bị tắc trong một cực trị địa phương mới. Các nghiên cứu của giáo sư Parisi chỉ ra rất nhiều tính chất của những hệ phức hợp như vậy. Điều thú vị là mặc dù kết quả của mỗi lần tương tác là khác nhau, không bao giờ lặp lại nhưng chúng ta có thể tìm ra các quy luật của sự khác nhau.
Trong thời gian sau này giáo sư Parisi cùng các cộng sự nghiên cứu tính đột phát của bầy chim sáo tạo thành các hình dạng cộng hưởng thú vị mà chúng ta thường thấy. Nhóm của ông đã chụp khoảng hơn 100 ngàn ảnh 3D của bầy chim sáo với số lượng từ vài trăm đến vài nghìn con (hình 3). Ông nói “các con chim sáo này rất thú vị vì chúng bay rất nhanh. Hàng ngàn con bay rất nhanh, rất thẳng và tạo ra được những hình thù kỳ dị. Câu hỏi đặt ra là chúng liên lạc với nhau như thế nào?”. Đây chính là một ví dụ điển hình về hệ phức hợp, và mặc dù là rất khác so với thủy tinh spin nhưng cũng có những điểm chung. Câu trả lời cuối cùng vẫn chưa có đầy đủ nhưng một số tính chất quan trọng của bầy chim đã được nhóm tìm ra.

Hình 4: Hình chiếu 2D của vận tốc (A) và chênh lệch vận tốc so với vận tốc trung tâm (B) của một bầy chim sáo.
Một trong số đó là sự tương quan mang tính phi tỷ lệ (scale-free correlation). Hình 4A cho thấy bản chiếu 2D của một bầy chim sáo với các mũi tên chỉ hướng của vận tốc. Phần lớn bầy chim đều bay theo một hướng với sự đồng nhất cao. Tuy nhiên trong hình 4B biểu diễn chênh lệch vận tốc của từng con so với vận tốc chung của cả bầy (vận tốc trung bình vector) thì ta nhận thấy có sự phân hóa thành hai nhóm, với mỗi nhóm có một vận tốc đại diện ngược nhau. Kết quả này cho thấy có cả sự tương quan đồng thuận (trong cùng nhóm) và sự tương quan ngược (giữa hai nhóm) trong cùng một bầy chim. Sự tương quan này phụ thuộc vào khoảng cách, đồng thuận ở khoảng cách gần và ngược ở khoảng cách xa. Ranh giới giữa hai vùng này xác định cho ta khoảng cách tương tác của chim sáo. Kết quả đặc biệt là khoảng cách này tỷ lệ với kích thước của bầy chim theo quy luật mũ (tính phi tỷ lệ). Ví dụ với một bầy chim có chiều rộng với chiều rộng không gian mà chúng chiếm lĩnh là 10 mét thì các con chim sáo chỉ liên lạc với các con trong phạm vi một mét gần nó. Trong khi với một bầy chim bay trên bầu trời với chiều rộng đàn 100 mét thì mỗi con sẽ liên lạc với các con khác trong phạm vi 10 mét gần nó. Chim sáo đã đoán nhận được số lượng của bầy, từ đó tăng tính tương tác của mình theo số lượng đó, nhưng bằng cơ chế nào?
Các phát triển kế tiếp của nhóm dựa trên tính bắt chước và tính tuân thủ quy luật chung của mỗi con chim, tuy nhiên mối quan hệ của chúng với khoảng cách tương tác có tính phi tuyến. Ở mức độ tuân thủ thấp thì tăng mức tuân thủ làm tăng khoảng cách tương tác nhưng đến một ngưỡng tới hạn nào đó, sự tuân thủ tăng lên nhưng bầy chim không tương tác xa hơn nữa mà dừng ở một ngưỡng nhất định.
Và ngoài các lĩnh vực trên ông còn nghiên cứu về lý thuyết dây, vật lý sinh học và thiết kế cấu trúc máy tính (cả phần cứng và phần mềm). Giorgio Parisi thường nói “Tôi hay nghiên cứu nhiều hướng cùng một lúc, bởi vì để có được ý tưởng cần có nhiều thời gian”.□
Bộ trưởng Bộ Khoa học Cristina Messa từng hứa hẹn sẽ tài trợ sáu tỉ euro cho 60 dự án, trong đó có năm tỉ đã được rót trong năm 2021. Theo dữ liệu năm 2019 cơ sở dữ liệu châu Âu Eurostat, Italy dành 1,45 % GDP cho nghiên cứu trong khi con số trung bình của EU là 2,19 %, cao nhất là Đức với 3,17%.
Nhưng lo ngại của Giorgio Parisi không chỉ có thế. “Italy không phải là ‘đất hứa’ cho nhà khoa học, dù là người Ý hay người nước ngoài cũng vậy”, ông nói. “Khoa học cũng như một vườn rau, nếu anh nghĩ anh chỉ cần tưới tắm cho nó hai lần một tuần thì kết quả thật tệ hại”.
Ông không quen nói suông mà không hành động. Ông tìm nhiều cách có thể để vận động cho ngân sách dành cho khoa học. Ông nhiều lần chỉ trích chính phủ Berlusconi vì sự cắt giảm ngân sách cho nghiên cứu khoa học khi cho rằng khoa học là xa xỉ trong thời gian khủng hoảng thay vì một cơ hội để có thể đưa đất nước vượt qua khủng hoảng.
Ông có những nguyên tắc nhất định trong suy nghĩ và hành xử, có thể gây khó hiểu ở người khác. Ông từng viết thư vận động sinh viên không đón tiếp Giáo hoàng Benedict XVI đến phát biểu khai giảng năm học mới ở Đại học Rome ở La Sapienza, một đại học hơn 700 năm tuổi. Ông viết “một chức sắc tôn giáo, dù chỉ là một giáo sĩ hay một lãnh tụ, cũng không nên đến phát biểu mở màn cho một tổ chức phi tôn giáo”.
Nhưng kể từ khi giải Nobel được xướng lên, tất cả đều chia vui cùng GS. Parisi và gia đình.
—–
Tham khảo
[1] Edwards SF, Anderson PW. 1975. Theory of spin glasses. J. Physics F: Metal Physics, 5, 965.
[2] Blandin A. 1978. Theories versus experiments in the spin glass systems. J. Phys. Coll. 39 C6, C6-1499-C6- 1516.
[3] Bray AJ, Moore MA. 1978. Replica symmetry breaking in spin-glass theories. Phys. Rev. Lett. 41,1068
[4] Parisi G. 1979. Toward a Mean Field Theory for Spin Glasses. Phys. Lett. A 73, 203.
[5] Parisi G. 1979. Infinite number of order parameters for spin-glasses Phys. Rev. Lett. 43, 1754.
[6] Hopfield JJ. 1982. Neural networks and physical systems with emergent collective computational properties. Proc. Nat. Acad. Sci. USA 79, 2554-2558.
Các tài liệu khác:
https://theconversation.com/my-phd-supervisor-just-won-the-nobel-prize-in-physics-heres-how-his-research-on-complex-systems-changed-science-169297
https://en.wikipedia.org/wiki/Giorgio_Parisi
https://www.pnas.org/content/103/21/7945
https://www.pnas.org/content/107/26/11865
https://physicsworld.com/a/giorgio-parisi-the-italian-activist/
————
1. Bài trên Tia Sáng http://tiasang.com.vn/-doi-moi-sang-tao/Khoa-hoc-he-phuc-hop-Giai-nhung-bai-toan-phuc-tap-cua-khoa-hoc-va-xa-hoi-24236
