Khoa học phức hợp – khoa học của thế kỷ 21

Đặc trưng quan trọng nhất của hệ thống phức hợp là gì?
Đó là hiện tượng đột sinh (emergence). Hiện tượng đột sinh là hiện tượng xuất hiện những quy luật, những hình thái, những trật tự mới từ hiệu ứng tập thể của các tương tác giữa các thành phần của hệ thống. Như vậy các hiện tượng đột sinh không phải là một tính chất nội tại của các thành phần con mà là những tính chất của hệ thống được xét một cách toàn cục.
–  Một minh họa là nhiệt độ và các định luật về chất khí – các khái niệm này vô nghĩa nếu ta chỉ xét một phân tử, chúng chỉ có ý nghĩa đối với một hệ nhiều phân tử.
–  Minh họa thứ hai là tổ chức quần thể loài kiến. Mỗi con kiến chỉ hành động theo những quy tắc rất địa phương (local) nhưng toàn thể xã hội loài kiến lại hành động theo những quy tắc đột sinh biểu hiện một trật tự cao. Hiện nay các nhà khoa học xã hội và tin học đang nghiên cứu hiện tượng tự tổ chức của xã hội loài kiến mong tìm ra những áp dụng khả dĩ cho xã hội chúng ta.
–  Một minh họa thứ ba là hiện tượng ùn tắc giao thông. Mỗi cá nhân tham gia giao thông có một kế hoạch riêng cho hành trình của mình, song nhiều cá nhân tham gia giao thông lại dẫn đến ùn tắc là một hiện tượng đột sinh không phụ thuộc vào kế hoạch của từng cá nhân.
Những ví dụ tinh tế hơn là “ý thức”, “sáng tạo”, hiện tượng đột sinh của hệ tế bào thần kinh.
Người ta thường nói: toàn cục lớn hơn tổng cơ học các thành phần để biểu diễn hiện tượng đột sinh. Và điều này cũng có nghĩa hệ thống là phi tuyến, những hệ quả bất ngờ đột xuất có thể xảy ra đối với một hệ thống phức hợp.
Vũ trụ chứa nhiều tầng lớp phức hợp liên quan đến nhau: thiên hà, thái dương hệ, các hành tinh, hệ sinh thái, sinh vật, tế bào, nguyên tử  rồi quark. Ta có những định luật riêng cho các tầng lớp phức hợp, các định luật đó là phổ quát (universal) đối với mỗi tầng phức hợp.
2. Một số định luật mô tả cách hành xử (behavior)  của hệ thống phức hợp
…   Fractal

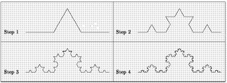
Fractal là một hình hình học mà mỗi yếu tố con của nó lại đồng dạng với toàn hình đó (xem hình 2). Sau đây là một ví dụ. Bước 1: lấy một đoạn thẳng xong vứt bỏ 1/3 đoạn thẳng ở giữa để thay vào đó một chữ V lộn ngược với hai cạnh bằng đoạn thẳng vứt đi (xem ô 1 bên trái trên). Bước 2: sau khi thu được hình ở bước 1, đối với mỗi đoạn thẳng ta lại thực hiện bước 2 giống như bước 1(xem ô 2 bên phải trên). Và liên tiếp như thế – cuối cùng ta thu được một fractal có hình đồng dạng với từng yếu tố con của nó (xem ô 4 bên phải dưới có được sau 4 bước). Đó là đường cong Koch. Không đi sâu vào định nghĩa toán học ta hãy chỉ ra số chiều D (dimension) của fractal dạng trên đây. Hình này dần chiếm nhiều chỗ trong mặt phẳng (số chiều là 2) song không chiếm hết được, fractal cũng chiếm nhiều chỗ hơn một đường thẳng (số chiều là 1) cho nên số chiều  của nó là
                                                 1< D < 2
Vậy fractal có số chiều không nguyên! Đây là một đặc trưng quan trọng của fractal.

 Dường như thiên nhiên rất tiết kiệm cho nên sáng tạo nhiều đối tượng theo cùng một quy tắc. Hình thái chia nhánh các cây, đường đi của không khí trong phế quản, hình dạng các bờ biển, các đám mây, các hoa, các núi (xem hình 3) đều có thể mô tả nhờ hình học fractal. Những hình dáng đó có tính chất bất biến đối với với phép thay đổi kích thước (scale-invariance). Hình học fractal do Benoợt Mandelbrots  (hình 4) xây dựng nên.
…   Định luật lũy thừa (power law)

Nếu thống kê số đám cháy rừng N  trong một quốc gia thì ta thu được công thức sau đây
                                       N  T S-a
Trong đó S là diện tích bị cháy, còn a là một số nằm giữa 1,3 và 1,5. Định luật lũy thừa trên có thể áp dụng cho nhiều hiện tượng như động đất, hoạt động của các vụ bùng nổ trên mặt trời… với a khác nhau cho nên định luật lũy thừa có tính phổ quát. Định luật này cũng có tính chất tự đồng dạng (self similarity). Quả thật như vậy nếu ta làm phép biến đổi S kS’ thì ta lại có ( k-a ).S’-a với ( k-a )= k’ là một hằng số.
Như vậy ta thấy sau fractal, lối hành xử theo định luật lũy thừa cũng là một lối hành xử phổ quát của một số  hệ thống phức hợp.
…  Định luật 1/ f
Trong nhiều hiện tượng người ta quan sát được định luật mô tả phổ các tần số
                                                   f – a
trong đó f là tần số, a là một hằng số. Ví dụ phổ các tần số tiếng ồn trong các mạch điện, thăng giáng điện thế trong các tế bào thần kinh, tần số đập của tim người… Như thế định luật 1/f cũng là một định luật phổ quát cho nhiều hệ thống phức tạp. Lúc a=1 (phổ biến) ta có định luật 1/f.
Chú ý tương tự như định luật lũy thừa định luật1/f cũng có tính tự đồng dạng.
Các định luật cơ học thống kê, nhiệt động học
Khi nghiên cứu một hệ nhiều hạt người ta không thể sử dụng tương tác vi mô giữa chúng để mô tả toàn hệ mà phải cầu cứu đến các định luật của cơ học thống kê, nhiệt động học. Đây là một minh họa về hiện tượng đột sinh (emergence) khi lối hành xử của một hệ không thể suy từ hành xử của từng hạt, của từng thành phần con.
Như thế có thể nói cơ học thống kê, nhiệt động học là những khoa học cổ điển nhất của lý thuyết về phức hợp. Chúng ta đã thay thế cách tiếp cận quy giản luận, vốn là cách tiếp cận dựa trên những định luật vi mô tất định bằng cách tiếp cận thống kê và xác suất đối với hiện tượng đột sinh.
Trên đây chúng ta chỉ nêu lên một số định luật đơn giản để mô tả các hệ phức hợp: hình học fractal, định luật 1/f, định luật lũy thừa (power laws), các định luật trong cơ học thống kê, xác suất, nhiệt động học. Các định luật đột sinh này tác động ở mức vĩ mô là đơn giản (có tính thống kê, xác suất) so với các định luật vi mô.
Mục tiêu của lý thuyết về phức hợp là tìm ra những định luật cao cấp hơn để mô tả nhiều hiện tượng khác, thậm chí tìm một lý thuyết thống nhất về phức hợp.

B .  CÂN BẰNG VÀ KHÔNG CÂN BẰNG(equilibrium & non-equilibrium)
Một khái niệm quan trọng trong lý thuyết về phức hợp là khái niệm tới hạn tự tổ chức (self-organised criticality). Theo khái niệm này các hệ phức hợp tự phát tiến triển về trạng thái tới hạn giữa bất trật tự và trật tự.
Việc tiến đến điểm tới hạn của quá trình tự tổ chức (self-organised criticality) là nguyên lý mà các hệ không cân bằng sử dụng để tự tổ chức mình vào một trạng thái nằm ở ranh giới bất trật tự (disorder) và trật tự (order). Như vậy các hệ thống không cân bằng sẽ tự xếp đặt mình vào một trạng thái tới hạn. Các tổ chức sống là những minh họa về những hệ thống này.
Các tổ chức sống là những hệ phức tạp nhất và một điều đáng lưu ý là các hệ này phát triển đến một trật tự cao cấp trái ngược với chiều mũi tên thời gian điều khiển bởi định luật thứ hai của nhiệt động học. Thật ra sự tăng độ mất trật tự và entropy do định luật thứ hai của nhiệt động học chỉ áp dụng đối với các hệ cân bằng kín. Các hệ sống không cân bằng và cũng không kín cần một dòng năng lượng để làm tăng trật tự (như vậy làm giảm entropy) cho bản thân song lại phát tán nhiệt và các chất thải để làm tăng bất trật tự (như thế làm tăng entropy) trong vũ trụ. Như thế i các hệ sống là những cấu trúc phát tán (dissipative structures) có khuynh hướng tiến đến tự tổ chức (self-organisation). Các hệ phát tán không phải là những hệ ở trạng thái cân bằng nhiệt động nhưng luôn có khuynh hướng tiến triển về cân bằng nhờ dòng entropy và năng lượng.
 Sự thoát khỏi trạng thái cân bằng là cần thiết để cho một cơ thể sống có thể có được một trật tự và hình thái phức hợp của nó.

C .  PHỨC HỢP VÀ HỖN ĐỘN(Complexity & chaos)
Phức hợp và hỗn độn là hai khái niệm gắn liền với nhau. Các hệ phức hợp nằm đung đưa ở ranh giới giữa hỗn độn và trật tự (balanced on the edge of chaos –not too orderly, not tooisordered). Cho nên việc nghiên cứu phức hợp gắn liền với lý thuyết hỗn độn.
Lý thuyết hỗn độn mô tả lối hành xử của một số hệ động học phi tuyến rất nhạy cảm với điều kiện ban đầu. Vì sự nhạy cảm này mà lối hành xử của hệ dường như hỗn độn, mặc dầu động học của nó được mô tả một cách tất định bởi những hệ phương trình vi phân.
Nhà khí tượng học Edward Lorenz đã sử dụng một mô hình để tính toán về khí tượng và phát  hiện khi điều kiện ban đầu thay đổi một ít thì kết quả tính toán lại phân kỳ so với nhau một cách đáng kể. Trong thực tế chúng ta không bao giờ biết được chính xác các điều kiện ban đầu cho nên bao giờ cũng rơi vào tình trạng không nắm kết quả cuối cùng chính xác. Đây là hiệu ứng gọi là hiệu ứng con bướm (butterfly effect): một con bướm đập cánh ở Aruba có thể gây nên bão lớn ở Bali! Hiện tượng trong đó một hệ hoàn toàn tất định có thể dẫn đến những hệ quả không tiên đoán được gọi là hỗn độn.
Các trạng thái của hệ phức hợp thường có thể mô tả bởi một hệ phương trình vi phân phi tuyến nối liền các đại lượng X, Y, Z,… (như nhiệt độ, áp suất,… và một số tham số a,b,c,… (như số Prandtl, số Rayleigh,… là những thông số kỹ thuật). Hệ phương trình này xác định cách hành xử của hệ phức hợp. Một điều kiện cần (chưa phải là đủ) cho hỗn độn là tính phi tuyến của hệ thống.
Hỗn độn là một tính chất của các hệ động học phi tuyến, đó là tính siêu nhạy cảm đối với các điều kiện ban đầu. Cho nên các hỗn độn quan sát được thật ra là hệ quả của một trật tự nằm trong không gian pha (X,Y,Z,…) tức không gian của các trạng thái (trong cơ học không gian pha là không gian tọa độ-xung lượng). Mỗi điểm trong không gian pha ứng với một trạng thái của hệ, các điểm đó làm thành quỹ đạo trạng thái. Nhiều hiện tượng tưởng chừng như ngẫu nhiên song đó là những hỗn độn của một hệ tất định.
Phần của không gian pha ứng với một hành xử nhất định của hệ phức hợp làm thành tập hút (attracting set) hay nói cách khác làm thành quỹ đạo hút (attractor) .
Quỹ đao hút có chu kỳ (periodic attractor)
Quỹ đạo hút có chu kỳ là một vòng lặp lại của các trạng thái. Ví dụ quỹ đạo của một hành tinh quanh một sao là một quỹ đạo hút có chu kỳ=1. Trên hình 5 là một quỹ đạo hút với chu kỳ = 4.

Quỹ đạo hút lạ (strange attractor)
Tính nhạy cảm đối với điều kiện ban đầu được biểu hiện ở sự phân kỳ các quỹ đạo trong không gian pha. Đối với các hệ phát tán khái niệm hỗn độn gắn liền với khái niệm quỹ đạo hút lạ (strange attractor): vì có hỗn độn cho nên các điểm mô tả trạng thái không nằm trên một quỹ đạo hút bình thường ví như quỹ đạo của một hành tinh quanh một sao, mà nằm trên một quỹ đạo hút lạ.
Chuyển động hỗn độn dẫn đến những quỹ đạo hút lạ (strange attractors).
 

Xét hệ mô tả bởi hệ các phương trình vi phân do nhà khí tượng học Edward Lorenz (hình 6) đề ra. Hệ này chứa ba đại lượng X,Y,Z và ba tham số a,b,c.  Khi a=28,b=10,c=8/3 thì chúng ta có một quỹ đạo hút lạ. Quỹ đạo hút lạ là một quỹ đạo hút không có chu kỳ. Trong không gian pha, quỹ đạo hút lạ có dạng ở hình 8 và là biểu hiện của hỗn độn.

Các tính toán thực hiện khi nghiên cứu các quỹ đạo hút lạ chủ yếu là những phép lặp mà người ta không thể thực hiện nổi bằng tay mà chỉ thực hiện được trên máy tính. Nhà hóa học Otto Rôssler (hình 7) đã thể hiện quỹ đạo hút lạ trên máy tính.
           

Hình 7: Otto Rôssler tác giả hệ phương trình mô tả các phản ứng hóa học dấn đến quỹ đạo hút lạ.

Không đi sâu vào định nghĩa toán học, chúng ta hãy xác định số chiều D của quỹ đạo hút lạ trên hình 8. Ta thấy các vòng này dày đặc chiếm gần hết không gian 3 chiều nhưng không chiếm hết! Mặt khác chúng cũng chiếm nhiều chỗ hơn không gian 2 chiều vì thế số chiều (dimension) của tâm hút này là:
                                         2 < D < 3
Đó là một đặc trưng của fractal: có số chiều D không nguyên.
Hai loại tâm hút có chu kỳ (periodic) và lạ (strange) được quan sát trong các hệ phát tán.
D/  PHỨC HỢP THEO QUAN ĐIỂM CỦA Chaitin & Wolfram
 

1. Thái độ hành xử của một hệ thống phức tạp có nguyên nhân từ hiện tượng đột sinh (emergence) và hiện tượng tự tổ chức (self-organisation).
Một mục tiêu của Stephen Wolfram (hình 9) trong cuốn sách “Một loại hình khoa học mới (A new kind of Science – NKS)” là giải thích thái độ hành xử của hệ thống phức hợp  xuất phát từ sự phát triển của các tế bào autômát. Wolfram tin tưởng rằng có một TOE (Theory of Everything- Lý thuyết của tất cả) và cho rằng phức hợp là hữu hạn.

2. Sau khi  Kurt Gôdel chứng minh rằng mọi toán học đều có những hạn chế (Định lý Không đầy đủ – Theorem of Incompleteness), rồi Alan Turing chứng minh rằng không tồn tại một chương trình  kiểm nghiệm (test) có thời gian hữu hạn để chứng tỏ rằng bất kỳ một chương trình máy tính nào cho trước sẽ dừng lại (Bài toán dừng -Halting Problem), Gregory Chaitin (hình 10)  đã phát triển một lý thuyết thông tin hiện đại, tìm ra số Omega () và đi đến khẳng định không thể tồn tại TOE  cho toán học và cho vật lý, điều này có nghĩa là sự hiểu biết về vũ trụ chứa đầy những lỗ trống bất khả tri. Vậy phức hợp là vô cùng. 

G. KẾT LUẬN

Các hệ phức hợp làm thành một chiếc cầu giữa cá nhân và tập thể: từ gen đến cơ quan sinh học, đến hệ sinh thái, từ nguyên tử đến vật liệu cần sản xuất, từ máy tính đến Internet, từ công dân đến xã hội. Khoa học phức hợp nối liền khoa học thuần túy với khoa học ứng dụng, xác lập những cơ sở mới để thiết kế, điều khiển, quản lý các hệ thống ở một trình độ cao hơn bất kỳ cách tiếp cận hiện nay.
Khoa học các hệ phức hợp còn là khoa học của máy tính cho nên ICT (Information & Communication Technologies- Công nghệ Thông tin & Truyền thông) là một bộ phận nghiên cứu quan trọng của khoa học phức hợp.
Các nước trong cộng đồng nghiên cứu phức hợp luôn khuyến nghị các nước khác (nhất là các nước thế giới thứ ba) cùng tham gia nghiên cứu phức hợp vì những ứng dụng của phức hợp rất to lớn và đã được kiểm nghiệm trong mọi lĩnh vực. Một trong những vấn đề thiết yếu đang gây nhiều chú ý ở Việt Nam có thể là giáo dục. Đây là một lĩnh vực cần tiếp cận dưới quan điểm khoa học phức hợp.