Một loại hình khoa học mới: 256 quy tắc để hiểu toàn bộ thế giới thực tại?

Stephen Wolfram là một nhà khoa học xuất sắc, nghiên cứu nhiều lĩnh vực (vật lý các hạt cơ bản, vũ trụ, toán học, tin học,…), tác giả của Mathematica, một phần mềm nổi tiếng được sử dụng trên toàn thế giới. Wolfram sáng lập tập đoàn phần mềm hàng đầu Wolfram Research,Tnc. Có trên 2 triệu người sử dụng Mathematica, nhiều phiên bản mới của Mathematica liên tục bảo đảm cuộc sống của hơn 300 người trong công ty Wolfram Research,Tn.

Hình 1 . Stephen Wolfram và cuốn sách đồ sộ dày 1280 trang Một loại hình khoa học mới (NKS)

Wolfram nhiều năm suy nghĩ về một câu hỏi lớn: mọi cấu trúc phức tạp và đa dạng trong thế giới thực tại đã hình thành như thế nào?  Liệu thiên nhiên có sử dụng một số quy tắc nào trong khi sáng tạo ra mọi vật, liệu có một khoa học lý thuyết nào để mô tả những quy tắc này? Trong thời gian sau này Wolfram rời quản lý công ty để chuyên nghiên cứu CA và năm 2002 công bố cuốn sách Một loại hình khoa học mới (A New Kind of Science viết tắt là NKS )[1] (dày 1280 trang); cuốn sách sớm trở thành hiện tượng trong giới khoa học (hình 1). Khi nói đến cuốn sách này người ta không thể không nói đến quyển Mathematica [2] (hình 2), cơ sở tính toán cho NKS.
Wolfram tin rằng tồn tại một chương trình rất đơn giản, nếu chạy trong một thời gian rất dài sẽ dẫn đến mọi phức tạp (complexity) trong vũ trụ: các sao, mặt trời, khí hậu, các sinh vật, các dòng chảy của chất lỏng, thị trường chứng khoán…Và chương trình đó chính là lý thuyết tối hậu của vật lý.
Nhiều người hỏi Wolfram các quy tắc mà ông đưa ra có dài dòng hay không? Wolfram trả lời rằng có lẽ chúng không dài dòng, trong ngôn ngữ Mathematica chúng chiếm chừng 3 đến 4 dòng. Wolfram hy vọng xuất phát từ những dữ liệu và điều kiện ban đầu đơn giản có thể tái tạo sự phức tạp của vũ trụ. Tham vọng của Wolfram rất lớn: giải thích toàn thể vũ trụ kể cả thế giới sinh vật, các dòng chảy,… thị trường chứng khoán. Và Wolfram đã tìm ra nhiều quy tắc cho sự phát triển của CA để thực hiện tham vọng của mình.
Theo Wolfram (và nhiều nhà khoa học khác) thì vũ trụ là không liên tục mà gián đoạn – giống như những bit trong thông tin cho nên ý tưởng về CA tức tế bào autômát là cơ bản. Họ muốn thiết lập mối quan hệ giữa vật lý và tin học [3].
Vũ trụ là một máy tính khổng lồ. Số phép tính mà vũ trụ thực hiện trong suốt lịch sử có thể lên đến 10120 trên lượng thông tin bằng 1090 bit [4]. Vũ trụ tính điều gì? Vũ trụ tính quá trình tiến triển động học của chính mình!
Trong lý thuyết CA của mình, Wolfram muốn chứng minh rằng với những quy tắc đơn giản chúng ta có thể thu được những hình thái rất phức tạp (kết quả này cũng thu được trong máy Turing [5]).
Gregory Chaitin, một nhà toán học lớn [6] đã phát biểu một cách ngưỡng mộ: Stephen Wolfram muốn phát hiện những viên gạch đầu tiên mà Chúa đã đặt xuống để xây dựng vũ trụ.

Hình 2 . Wolfram và cuốn Mathematica nổi tiếng

1/ Tế bào autômát (CA) cơ bản
Tế bào autômát là đơn vị nằm trong một ô mạng gián đoạn sử dụng cho tính toán. CA cơ bản có một chiều (dimension), mỗi tế bào có 2 trạng thái: 1 & 0 hay đen & trắng, mỗi tế bào có 2 tế bào lân cận nằm hai bên. Sở dĩ các tế bào này được gọi là autômát vì chúng tự động phát triển trong thời gian theo những quy tắc nhất định.

Hình 3 . Kết quả áp dụng 110 sau 10 lần lặp

Như vậy với các CA cơ bản ta có một tập gồm 3 tế bào vậy có 23 = 8 cấu hình cho một tập như thế. Sau đây là 8 cấu hình của các tập 3 tế bào (ở hàng một ta dùng số 1 & 0 để chỉ trạng thái, ở hàng dưới ta dùng màu đen & trắng để chỉ trạng thái):

Bảng1: quy tắc110,trạng thái biểu diễn bằng màu: đen (ứng với số1)& trắng (ứng với số 0)

2/ Sự phát triển của CA theo thời gian
Lấy một tế bào đen trên hàng thứ nhất (xem hình 3).
Trên hàng thứ hai (ứng với thời điểm tiếp theo, như thế không gian và thời gian quyện với nhau) ta lấy thêm một tế bào bên trái, vậy ta có hai tế bào, chúng có màu đen hay màu trắng? Trạng thái mới của tế bào phụ thuộc vào trạng thái trước của nó và của hai tế bào lân cận. Ta phải lấy một quy tắc nào đó để gán màu cho chúng. Sau đây ta dùng quy tắc gọi là quy tắc 110 biểu diễn ở bảng 1. (Vì sao gọi là quy tắc 110, xin xem chú thích [7]).
 Màu của tế bào nằm ở hàng tiếp theo tùy thuộc vào các màu của 3 tế bào nằm đúng trên nó một hàng (tế bào nằm dưới ở ngay vị trí giữa của 3 tế bào nằm trên). Theo quy tắc nêu ở bảng 1: ví dụ 3 tế bào nằm trên có cấu hình 111 thì tế bào nằm dưới sẽ là tế bào 0 tức là tế bào trắng, nếu trên có cấu hình 110 thì tế bào dưới sẽ là tế bào đen và…
Sau 10 lần lặp (lấy liên tiếp 10 hàng) ta có hình 1, sau 700 lần lặp ta có hình 2.

Hình 4. Kết quả áp dụng quy tắc 110 sau 700 lần lặp

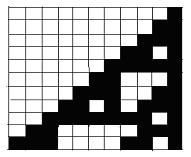
Có bao nhiêu quy tắc như quy tắc 110 mà chúng ta vừa áp dụng? Vì mỗi tế bào có hai trạng thái cho nên đối với một tập 8 tế bào (xem hàng thứ hai ở Bảng 1) số cấu hình khác nhau sẽ cho ta số quy tắc bằng:  28 = 256  quy tắc.
Wolfram cho rằng sử dụng 256 quy tắc cho sự phát triển của CA, chúng ta có thể tái tạo mọi sự phức tạp (complexity) trong vạn vật. Trong 256 quy tắc đó, quy tắc 110 (và quy tắc 30 [ 7 ]) là lý thú nhất.
Chú ý : Các CA có thể có dạng hình học khác (không phải hình vuông mà ví dụ là hình lục giác) và số chiều của CA có thể lớn hơn 1 (xem hình 5 ).

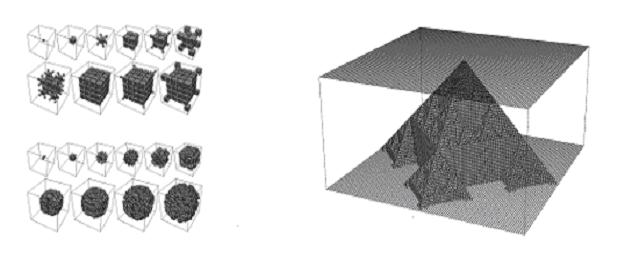
Hình 5 . Ví dụ CA trong 3D (3 chiều) tạo nên bởi CA  2D phát triển trong thời gian.

Stephen Wolfram nếu không phải là người duy nhất có tư tưởng về các tế bào autômát thì cũng là người làm hồi sinh ý tưởng này trên một bình diện mới mẻ và phổ quát.
Nội dung của NKS bao trùm từ những hiện tượng chảy của chất lỏng, sự tăng trưởng của các tinh thể, … đến diễn biến của thị trường chứng khoán, và cũng không để ngoài các định luật trong cơ lượng tử, lý thuyết tương đối rộng và thậm chí lĩnh vực  nghệ thuật.
Theo Wolfram sự phức tạp (complexity) nảy sinh từ những điều đơn giản.
Wolfram phát biểu: các tế bào autômát là những máy tính phổ quát (universel), điều đó có nghĩa là chúng có thể mô phỏng mọi phép tính (operation): từ phép cộng đến thuật toán tạo dãy số ngẫu nhiên.
Từ bản chất là những đối tượng tin học, những tế bào autômát có khả năng tiếp cận đến vật lý, sinh học và  triết học.

3/ Một số ví dụ minh họa
 a. Cháy rừng: có thể tái tạo quá trình rừng cháy bằng CA, mỗi tế bào có bốn trạng thái (không có cây, có cây xanh, có cây đang cháy, cây đã cháy thành than). Cơ quan CIRID (Cơ quan hợp tác quốc tế phát triển nông nghiệp) đã dùng lý thuyết CA để tạo cháy rừng ảo để khảo sát hiện tượng cháy rừng.
b. Nam châm từ: mỗi tế bào có 2 trạng thái (từ trường hướng lên trên và hướng xuống dưới). Sử dụng lý thuyết CA có thể tái tạo chuyển pha loại hai (tức là loại chuyển pha liên quan đến phá vỡ đối xứng).
c. Các đa dạng trong thế giới tự nhiên và sinh học.
Xem hình 6 ta bất giác tự hỏi , từ đâu đến sự phức tạp và vẻ đẹp của các bông tuyết? Thế nhưng trong khuôn khổ các tế bào autômát Wolfram có thể tái tạo những hoa văn đó của tự nhiên (xem các hình 7,8).
Sự hình thành các dạng sinh học của cây cối, các sắc tố có dạng hoa văn trên vỏ sò, nhiều hình fractal [8] cũng có thể thu được nhờ sự phát triển của các CA (xem các hình 9,10). Nhiều hoa văn thu được từ CA cũng được sử dụng trong mỹ thuật trang trí (xem hình 11).
   
a. Sự sống
Năm 1970 nhà toán học người Anh John Conway sử dụng CA trong không gian 2 chiều, mỗi tế bào có 8 tế bào lân cận và mỗi tế bào có hai trạng thái: chết (tế bào đen) và sống (tế bào trắng) để xây dựng trò chơi: Trò chơi sự sống. Quy tắc chơi: một tế bào chết sẽ trở thành tế bào sống nếu có 3 tế bào lân cận là tế bào sống, một tế bào sống sẽ sống nếu có ít nhất 2 tế bào lân cận là tế bào sống.
Trò chơi này được Christopher Langton nâng cấp thành một phiên bản tinh xảo với ý đồ nghiên cứu “trí khôn nhân tạo”. Nếu cho chương trình của phiên bản này chạy một điều kỳ diệu đã xảy ra: một cá thể (individu-tập một số tế bào) có thể tạo sinh ra một cá thể khác đồng nhất với nó.
Liệu Stephen Wolfram có sử dụng những ý tưởng trên khi phát hiện ra 256 quy tắc của mình đối với các tế bào autômát một chiều? Trong khi áp dụng lý thuyết tế bào autômát vào sự sống Wolfram cho rằng sự phức tạp trong thế giới sinh học ít liên quan đến thuyết chọn lọc tự nhiên (sélection naturelle) mà là kết quả của dãy biến thiên của các tế bào autômát.
Ngoài ra Jean-Philippe Rennard, nhà tin học tác giả cuốn sách “Sự sống nhân tạo” đã phát biểu: “Đóng góp lớn của lý thuyết các tế bào autômát  Wolfram là phát hiện hiện tượng đột sinh (émergence).  Đột sinh trong lý thuyết tiến hóa là sự xuất hiện những hệ thống không thể đoán trước hoặc giải thích trên cơ sở những điều kiện trước đó.
b. Thị trường chứng khoán
Từ đâu phát sinh những biến động ngẫu nhiên trên thị trường chững khoán. Lẽ dĩ nhiên một nguyên nhân là tác động của môi trường song một nguyên nhân khác là ngẫu nhiên đã phát sinh một cách nội tại. Wolfram trong lý thuyết CA của mình đã minh họa được sự phát sinh những ngẫu nhiên nội tại (intrinsic randomness) nhờ quy tắc 30.
c. Vũ trụ
Theo Wolfram vũ trụ tuân theo một quy tắc thống nhất, đơn giản, tiềm ẩn.
Từ trước nhà vật lý lý thuyết nỗi tiếng Richard Feynman, giải Nobel năm 1965 đã đưa ra ý tưởng về một vũ trụ-máy tính. Trong thời gian hiện nay các nhà vật lý đã xây dựng nhiều lý thuyết phức tạp thống nhất lượng tử và hấp dẫn như lý thuyết dây.
Trong khuôn khổ lý thuyết tế bào autômát Wolfram không cần đến những định luật phức tạp. Vũ trụ đã chạy chương trình các tế bào autômát từ thuở nguyên sinh. Một nhà vật lý muốn thử nghiệm điều này phải cần một thời gian tương tự và một không gian lớn như vậy. Ngoài ra cần một lý thuyết tế bào autômát nhiều chiều với một cấu trúc không thời gian phức tạp.
Wolfram cho rằng các định luật vật lý tìm ra đến nay đều không là cơ bản mà chỉ là những tính chất đột sinh từ các quy tắc tiềm ẩn trong lý thuyết các tế bào autômát.
d.  Hấp dẫn
Chúng ta có thể mô tả không gian phẳng bằng một mạng CA có hình lục giác (xem hình 12)
Hình 12 . Mạng CA hình lục giác
Song nếu ta đưa vào mạng của các ô lục giác những ô ngũ giác và thất giác  (5&7 cạnh), ta sẽ thu được không gian cong (xem hình 13) trong lý thuyết  hấp dẫn.
Hình 13 . Mạng CA có chen những hình 5 & 7 cạnh vào mạng gốc chứa các hình lục giác mô tả không gian có độ cong.
e. Vật lý hạt cơ bản
Xem hình 3 ta thấy rằng ngoài những cấu trúc mang tính đều (xem mép trái của hình 4) chúng ta còn thấy xuất hiện những cấu trúc mới đột sinh (xem mép phải của hình 4). Trong lý thuyết CA, Wolfram có thể thu nhận được những cá thể như ở hình 14 nhờ quy tắc 110. Trên hình này có thể đoán nhận sự tương tác của các hạt theo sơ đồ Feynman.
Hình 14 . CA mô tả tương tác của các hạt cơ bản

4/ Các phản biện
Cuốn sách A new kind of  Science- NKS  có thể xem là một hiện tượng. Các báo chí đã không ngớt lời ngợi khen. Sau đây là sự đánh giá của các báo lớn trên thế giới.
New-York Times: Đây là tác giả đã làm chấn động khoa học.
Frankfurter Allgemeine Zeitung: Newton,Einstein hay Wolfram?
Time: Như vậy vạn vật được giải thích.
Newsweek: Những bộ óc lớn, những tư tưởng lớn.
The Daily Telegraph: Wolfram mạnh hơn cả Newton và Darwin?
Personal Computer World: Thế giới dưới con mắt của Wolfram.
New Scientist: Đây là cuốn sách của những khám phá.
Tuy nhiên nhiều nhà khoa học đã phản đối mạnh mẽ NKS vì 2 lý do:
a. Trong cuốn sách của mình Wolfram đã viết nhiều lời thiếu khiêm tốn khi cho rằng “ đây là một trong những phát hiện quan trọng nhất trong lịch sử khoa học lý thuyết”. Ngoài ra Wolfram không  trích dẫn những công trình trước dẫn đến ý đồ của mình. Nhiều người còn cho đây là một cử chỉ có thể bị kết tội  “đạo văn” (thực tế thì Wolfram chỉ phạm lỗi thiếu trích dẫn nhiều công trình quan trọng trước mình còn những đóng góp của Wolfram là rất mới mẻ và độc đáo).
Trong lịch sử Stanislaw Ulam & John von Neumann là các tác giả của tế bào autômát.
Nhà toán học Edward Fredkin trong những năm 60 cũng đã đưa ra ý tưởng về những tế bào autômát  và sự tồn tại những quy tắc phát triển đơn giản của các tế bào đó để giải thích nhiều hiện tượng.
Nicolas Metropolis, Paul Stein & Myron Stein đã đề cập đến vấn đề tính phức tạp (complexity) có thể phát sinh từ sự lặp lại của những quá trình đơn giản.
John Conway đã đưa ra một trò chơi tin học trở thành thịnh hành trong sinh viên: Trò chơi sự sống như trên đã nói.
b. Khi nghi ngờ quy luật chọn lọc tự nhiên, Wolfram đã không nói tường minh rằng các kết quả của ông ở mức hệ gen (genome) hay ở mức tế bào. Theo nhiều tác giả lý thuyết CA không thể nói đến các hoạt động phức tạp của não bộ, của hệ miễn dịch, của quá trình biến dưỡng (metabolisme) của tế bào. Trong khi đó chính những quy luật chọn lọc tự nhiên (selection naturelle) và thích nghi (adaptation) lại cần thiết để hiểu các vấn đề này.
Về nguyên lý tương đương tính toán (computational equivalence) do Wolfram đưa ra khẳng định rằng mọi hệ thống đều thực hiện những chương trình tính toán và có thể đạt đến mức cao nhất của công suất tính toán thì Melanie Mitchell [9] cho rằng con người và con giun Caenorhabditis elegans [10] có thể đều thực hiện những chương trình tính toán song các phép tính thực hiện không thể đồng cấp về mức phức tạp.
Tác giả Ray Kurzweil [11] cho rằng một điểm yếu của lý thuyết CA của Wolfram là thiếu khả năng tiên đoán, qua một số lặp người ta không thể biết trước điều gì sẽ xảy ra.
Thứ hai, các cấu trúc đã xuất hiện sẽ tái xuất nhưng mức  phức tạp (order of complexity) không tăng lên, vậy khó lòng tạo nên sinh vật, con người hoặc bản dạo khúc của Chopin.
Theo Ray Kurzweil lý thuyết CA của Wolfram cần bổ sung quy tắc liên quan đến thuật toán tiến hóa (evolutiary algorithm). Nhờ thuật toán này lý thuyết mới có khả năng chọn lời giải thích ứng nhất với môi trường và như thế mở khả năng dẫn đến mức phức tạp cao hơn.
Ngoài ra một vấn đề quan trọng khác là mối liên hệ giữa liên tục (mô tả bởi toán học cổ điển cùng với các phương trình vi phân) và gián đoạn mô tả trong lý thuyết CA. Dường như thiên nhiên dao động giữa tương tự (analog) và số hóa (digital). Các transistor có thể điều khiển những electron như một thiết bị số hóa song nếu xét ở mức sâu hơn chúng ta cần những phương trình tương tự của lý thuyết lượng tử. Nhiều đối xứng trong thiên nhiên như đối xứng quay, đối xứng tịnh tiến, đối xứng Lorentz, đối xứng điện yếu và nhiều đối xứng khác là liên tục và khó lòng được mô tả trong khuôn khổ của vật lý số hóa. Đây là một vấn đề lớn về vật lý và triết học: liệu có thể quy mọi quá trình về các quá trình số hóa?

5/ Kết luận
Số người phản đối NKS không phải là ít. Tuy thế  ý tưởng táo bạo của Stephen Wolfram vẫn là hấp dẫn đối với nhiều nhà khoa học ít nhất vì lý thuyết CA của Wolfram đã đề cập đến câu hỏi sâu kín nhất của khoa học và triết học: mọi hình thái của thực tại từ đâu đến? NKS có thể là cái phôi nào đó của một chân lý lớn.
Nhiều nhà khoa học cho rằng Wolfram đang đi đúng đường[9] và lý thuyết CA của Wolfram xứng đáng được gọi là một loại hình khoa học mới, một NKS.
Ray Kurzweil trong cuối bài phát biểu [11] cho rằng cuốn Một loại hình khoa học mới của Wolfram là một công trình quan trọng về bản thể học (ontology)[12]. Thời gian từ lúc công bố NKS còn quá ít để có thể đánh giá đúng đắn giá trị của nó.
 

Tài liệu tham khảo & chú thích

[1]   Stephen Wolfram, A new kind of Science: NKS | ON LINE, 2007
[2]   Stephen Wolfram, Mathematica
[3]   David Larousserie, Le nouveau jeu de la vie, Science et Avenir, tháng 1/năm 2003
[4]   Olivier Postel -Vinay & . L’Univers est-il un calculateur? La Recherche, tháng 1/ năm 2003
[5]   Máy tính trừu tượng nhận thức bởi Alan Turing có khả năng về mặt lý thuyết thực hiện mọi tính toán
        toán học.
[6]   CC .  Có thể hiểu vũ trụ?  Tia Sáng số 17 – 05/09/2006
[7]   Tại sao quy tắc này có tên là quy tắc 110?
        Hãy nhìn dãy số ứng với trạng thái của tế bào nằm giữa trên hàng dưới (bảng 1):
        01101110= trong hệ nhị phân dãy số này bằng =
        0.27 + 1.26+ 1.25 + 0.24 + 1.23 + 1.22 +1.21 + 0.20  =  64+32+8+4+2 =110
       Vì thế quy tắc này gọi là quy tắc 110.
        Nếu dãy số ứng với trạng thái của tế bào nằm giữa trên hàng dưới cua bảng 1 lại là : 00011110 thì
        chúng  ta có quy tắc 30.
[8]   Fractal là một hình hình học mà mỗi phần của nó lại đồng dạng với toàn hình đó (Benoit Mandelbrot,
       1975), fractal có số chiều không nguyên (theo định nghĩa số chiều của Felix Hausdorff).
[9]   Melanie Mitchell .Quelques raisons de douter, La Recherche, tháng 1/ năm 2003
[10] Caenorhabditis elegans là một loài giun đa bào đầu tiên.
[11] Ray Kurzweil, Reflections on S.Wolfram’s NKS
        http://www.kurzweilai.net/articles/art0464.html?printable=1
[12] Môn triết học nghiên cứu bản chất của sự sống, của thực tại, của sự hiện hữu