Cơ học lượng tử và công nghệ thông tin
Cơ học lượng tử có nhiều điểm kỳ lạ, không dễ nhận ra bằng trực quan. Đó là những vấn đề như hiện thực (realism), phi định xứ (non locality) và liên đới lượng tử (quantum entanglement). Song những điều kỳ lạ này của cơ học lượng tử lại xuất hiện như những điều kỳ diệu trong Công nghệ tin học (CNTH)[1].

Ba nhà vật lý: Alain Aspect (Pháp), John F. Clauser (Mỹ), Anton Zeilinger (Áo) năm 2010 được trao giải Wolf về nghiên cứu liên đới lượng tử.
Quan điểm hiện thực (realism)
Như chúng ta biết cơ học cổ điển chỉ ứng dụng được đối với thế giới vĩ mô. Đối với thế giới vi mô (thế giới các hạt cơ bản) phải ứng dụng CHLT. Từ năm 1920 CHLT đã mô tả thế giới vi mô với độ chính xác cao. Song nhà vật lý lớn của mọi thời đại là Einstein đã không thừa nhận CHLT. Einstein có lý hay không? Những thí nghiệm trong năm 2007 chứng tỏ rằng Einstein đã sai lầm. Các thí nghiệm này cho chúng ta biết rằng: các tính chất của các hạt “không tồn tại” trước khi các tính chất đó được quan sát bởi một thiết bị đo đạc.
Theo cơ học lượng tử thì một hạt cơ bản không có một tính chất xác định ví dụ hình chiếu của spin trên trục z: σz hoặc trên trục x: σx cho đến khi chúng ta thực hiện một phép đo thích hợp để tìm đại lượng tương ứng.
EPR (Einstein,Podolsky, Rosen) phủ nhận nhận định đó, cho rằng hạt có những tính chất nhất định không phụ thuộc vào phép đo, đó là quan điểm gọi là hiện thực (realism): hạt đã có trước một tính chất nào đó trước phép đo!
Liên đới lượng tử (quantum entanglement)
Thế nào là liên đới lượng tử?
Theo cơ học lượng tử, người ta có thể chế tạo một cặp hạt liên đới lượng tử (quantum entangled), hay còn gọi là cặp EPR điều đó có nghĩa về mặt toán học đây là một cặp hạt mà hàm sóng f của chúng không thể viết thành tích trực tiếp hàm sóng của từng hạt: f không bằng f1 nhân trực tiếp với f2 , hay nói cách khác là các tính chất của các hạt không độc lập với nhau mà liên quan với nhau.
Có thể chế tạo một cặp hạt EPR hay không?
Nhà vật lý Pháp Alain Aspect đã đưa ra một phương pháp đơn giản để chế tạo cặp hạt liên đới lượng tử: khi một xung laser bắn vào một tinh thể có những tính chất gọi là “phi tuyến”, thì một photon biến thành một cặp photon liên đới lượng tử (với độ dài sóng lớn hơn).
Ngoài ra hai photon có thể liên đới lượng tử nếu được sinh ra ví dụ từ phân rã của hạt p-meson trung hòa.
Phi định xứ (non-locality)
Tính chất lạ lùng của cặp hạt liên đới lượng tử
Cặp hạt liên đới lượng tử có một tính chất lạ lùng phát hiện bởi Einstein trong những năm 30 của thế kỷ trước: hai thực thể liên đới lượng tử dường như được nối liền với nhau bởi một sợi dây vô hình, bí ẩn, dầu tách chúng xa nhau đến mức nào, trị riêng đo được của hạt này lại phụ thuộc vào trị riêng đo được của hạt kia, cho dù rằng chúng được tách rời nhau đến vô cực! Hiện tượng ảnh hưởng của phép đo thực hiện trên một hạt này đối với hạt cách xa là một hiện tượng “phi định xứ” (non-locality).
Einstein đã gọi hiện tượng này là một tác động ma quái ở khoảng cách (spooky action at a distance). Đây là một hiện tượng thuần túy cơ học lượng tử. Trong những năm gần đây hiện tượng liên đới lượng tử mở ra những triển vọng to lớn về viễn tải lượng tử, tính toán lượng tử và mật mã lượng tử [2].
Nghịch lý EPR (Einstein, Podolsky, Rosen)
Sự chống đối cơ học lượng tửlên đến đỉnh cao khi Einstein cùng Podolsky và Rosen đưa ra cái gọi là nghịch lý EPR (lấy theo chữ đầu từ tên của ba người). Tên bài báo là: Liệu sự mô tả thực tại vật lý bằng CHLT có thể xem là đầy đủ hay không? (Can QM Description of Physical Reality Be Considered Complete?).
Nội dung của nghịch lý có thể tóm tắt như sau.
Theo CHLT người ta có thể chế tạo một cặp hạt liên đới (entangled) lượng tử. Xét hai hạt liên đới lượng tử và tách chúng ra xa nhau. Khi đo tọa độ của hạt thứ nhất thì sẽ biết được tọa độ của hạt thứ hai, vì chúng liên đới lượng tử. Song bây giờ lại đo xung lượng của hạt thứ hai ta lại có thể biết được xung lượng của hạt thứ nhất. Như thế ta có thể đồng thời đo được tọa độ lẫn xung lượng của mỗi hạt: điều này trái với nguyên lý bất định Heisenberg của cơ học lượng tử. Đó là nghịch lý EPR.
Lý luận trên dựa trên hai giả thuyết:
1/ Giả thuyết hiện thực (realism): hạt có một tính chất khách quan trước khi ta thực hiện phép đo tính chất đó,
2/ Giả thuyết định xứ (locality): phép đo trên hạt thứ nhất không ảnh hưởng đến kết quả phép đo trên hạt thứ hai, mặc dầu chúng cách xa nhau.
Bohr đã trả lời EPR vài tuần sau khi EPR công bố nghịch lý nói trên. Trong bài trả lời, Bohr phủ nhận giả thuyết hiện thực (tuy rằng có một ít yếu tố mơ hồ trong bài trả lời, song Bohr đã đi đúng đường). Theo Bohr CHLT có thể biết được các tính chất của hạt trong điều kiện thực hiện phép đo các tính chất đó. CHLT không mô tả thực tiễn theo ý tưởng tiên quyết của chúng ta. Bohr cho rằng vô nghĩa khi gán cho hạt một tính chất nào đó mà lại tách rời khỏi các điều kiện thực nghiệm cho phép đo được tính chất đó.
Bất đẳng thức Bell
Năm 1964 John Bell tìm ra bất đẳng thức gọi là bất đẳng thức Bell và nhờ những bất đẳng thức đó chứng minh rằng những giả thuyết hiện thực và định xứ (trong đó có cả các lý thuyết định xứ với tham số ẩn) đều không phù hợp với cơ học lượng tử.
Thế nào là bất đẳng thức Bell?
Sau đây là một thí nghiệm để suy ra bất đẳng thức Bell.
Charlie chuẩn bị 2 hạt (không quan trọng là Charlie đã chuẩn bị như thế nào) và gửi cho Alice & Bob mỗi người một hạt (hình 1).
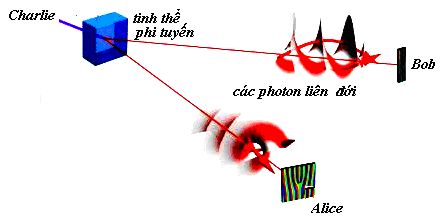
Hình 1. Charlie chuẩn bị hai hạt liên đới và gửi cho Alice và Bob mỗi người một hạt
Alice &Bob mỗi người thực hiện hai phép đo. Và kết quả các phép đo cho hoặc +1 hoặc -1. Gọi các trị số Alice thu được là Q và R, còn Bob thu được là S và T. Nếu thực hiện các phép tính theo tư duy hiện thực và định xứ thì một tổ hợp nhất định các giá trị trung bình của Q, R, S & T phải nhỏ hơn hoặc bằng 2. Đó là bất đẳng thức Bell. Còn nếu tính toán theo CHLT đối với hai hạt liên đới lượng tử thì lại thu được số 2√2=2,82843 cho tổ hợp đó [2].
Các dữ liệu thực nghiệm cho thấy rằng bất đẳng thức Bell không đúng còn các kết quả tính theo CHLT là chính xác.
Hai vấn đề gắn liền với bất đẳng thức Bell:
(1). Cho rằng Q, R, S, T tồn tại độc lập với các phép đo. Đó là quan điểm hiện thực (realism).
(2). Việc giả định rằng Alice khi tiến hành phép đo không ảnh hưởng gì đến kết quả các phép đo do Bob thực hiện. Đó là quan điểm định xứ (locality).
Hai quan điểm trên kết hợp lại thành quan điểm hiện thực định xứ (local realism). Bất đẳng thức Bell không đúng với thực tế và như vậy ít nhất một trong hai quan điểm nói trên là sai lầm. Đây là bài học lớn cho chúng ta: vũ trụ không hiện thực định xứ!
Sự vi phạm bất đẳng thức Bell cho chúng ta thấy rằng:
Cơ học lượng tử là đúng và hiện tượng liên đới lượng tử (quantum entanglement) là một nguồn sức mạnh mới cho khoa học và công nghệ vì hiện tượng liên đới lượng tử làm đột sinh một ngành mới quan trọng đó là lý thuyết thông tin lượng tử (Quantum Information Theory) dẫn đến ngành mật mã lượng tử (Quantum cryptography).
Bất đẳng thức Leggett
Nhiều nhà vật lý cho rằng nên giữ lại quan điểm hiện thực (realism), mà từ bỏ quan điểm định xứ (locality).
Người ta giả sử rằng hai photon liên đới lượng tử có một trạng thái phân cực (polarisation) xác định, nghĩa là tuân theo hiện thực luận.
Người ta loại giả thuyết định xứ bằng cách cho rằng tồn tại một tác động ở khoảng cách vô cùng (phi định xứ), một tác động ma quái (spooky action) mà Einstein đã nói đến.
Nhà vật lý giải Nobel 2003 Anthony Leggett đã tìm ra một hệ các bất đẳng thức (tương tự như bất đẳng thức Bell) đối với các phép đo các mối liên quan của hai hạt photon nói trên cho những lý thuyết không định xứ song vẫn dựa trên hiện thực luận.
Thí nghiệm thực hiện năm 2007 của Anton Zeilinger (và nhiều người khác), lại loại trừ một lớp lý thuyết không định xứ song theo hiện thực luận vì vi phạm hệ bất đẳng thức Anthony Leggett. Vậy hy sinh định xứ luận không đủ cứu vãn hiện thực luận.
Nói cách khác các thí nghiệm đều dẫn đến kết quả phủ nhận hiện thực luận lẫn định xứ luận.
Cơ học lượng tử là đúng và hiện tượng liên đới lượng tử là một nguồn sức mạnh mới cho khoa học và công nghệ.
Máy tính lượng tử
Qubit (quantum bit), bit lượng tử là gì?
Chúng ta đã biết bit là một thực thể vật lý, có thể lấy 2 trạng thái mà trong kỹ thuật số ta gọi là 0 và 1.
Một bit lượng tử được viết tắt là qubit (hoặc qbit). Song một điểm khác nhau giữa bit và qubit là: ngoài hai trạng thái 0 và 1, qubit còn có nhiều trạng thái trung gian giữa 0 và 1 làm thành một tổ hợp tuyến tính của 0 và 1.
Như vậy qubit có cả một continuum trạng thái giữa 0 và 1. Người ta có thể thực hiện qubit nhờ hai trạng thái phân cực của photon, có thể nhờ hai hình chiếu spin của một electron…
Người ta cũng có thể xét hệ nhiều qubit. Hai qubit có các trạng thái 00, 01, 10 và 11 do đó có trạng thái tổng quát là tổ hợp tuyến tính của các trạng thái đó.
Sức mạnh của máy tính lượng tử ở đâu? [2]
Bước cơ bản trong tính toán lượng tử là phép toán unita U trên trạng thái chồng chất l-qbit. Phép toán U được thực hiện song song đối với tất cả 2exp(l) biên độ phức. Trong máy tính cổ điển một phép toán như vậy đòi hỏi 2exp(l) bước tính cơ bản cho mỗi biên độ.
Chính tính chất song song lượng tử này trong các máy tính lượng tử dẫn đến một gia tốc hàm mũ cho quá trình tính toán. Đây là ưu thế tuyệt đối của máy tính lượng tử so với máy tính cổ điển thông dụng hiện nay.
Viễn tải lượng tử (teleportation)
Có thể chăng làm biến mất một con người tại một điểm, để rồi tái tạo con người đó tại một điểm khác? Đây là khoa học hay viễn tưởng?
Phim khoa học viễn tưởng nhiều tập Star Trek đã dựng nên một viễn cảnh khoa học giàu tưởng tượng. Thuyền trưởng Kirk nhờ thuyền phó bấm một số nút và Kirk đã phi vật chất hóa (dematerialise) thành một tia chớp ánh sáng để xuất hiện trên một hành tinh bí ẩn.
Viễn tải (teleportation) từ lâu là một câu chuyện khoa học viễn tưởng. Đến năm 1992 một nhóm các nhà vật lý và tin học đã tìm ra ý tưởng để sao chép một trạng thái của một hạt đến một nơi khác. Họ đã sử dụng một hiện tượng do Einstein phát hiện trong những năm 30 của thế kỷ trước: trong một số điều kiện, hai thực thể lượng tử lại được nối liền với nhau (liên đới lượng tử – quantum entanglement) bởi một sợi dây vô hình, bí ẩn.
Trong những năm gần đây người ta đã tiến hành những thí nghiệm chứng tỏ viễn tải lượng tử là vấn đề khoa học nghiêm chỉnh, mở ra những khả năng rộng lớn cho tính toán lượng tử, mật mã lượng tử.
Quá trình viễn tải thực hiện như được mô tả ở hình 2.
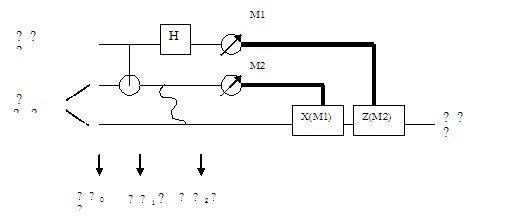
Hình 2. Trên hình là mạch lượng tử để viễn tải một qubit. Dòng trên hết là qubit 1 mà ta muốn viễn tải trạng tháí. Dòng thứ hai là qubit 2 ứng với hạt 2 trong cặp EPR mà Alice giữ lại bên mình. Dòng thứ 3 là qubit 3 ứng với hạt 3 trong cặp EPR mà Alice đã gửi cho Bob. M1 và M2 là các phép đo. Đường kép ứng với thông tin cổ điển. Đường sóng chỉ rằng qubit 2 và 3 là liên đới lượng tử.
Lẽ dĩ nhiên, Bob cần có thông tin từ Alice để biết kết quả đo của Alice, vậy Alice phải dùng một kênh thông tin cổ điển để báo cho Bob biết kết quả đo của mình, như thế Alice cũng không viễn tải trạng thái Ψ nhanh hơn ánh sáng được!
Như vậy với viễn tải lượng tử cần chú ý hai điều:
1. Không thể chuyển thông tin nhanh hơn tốc độ ánh sáng.
2. Trạng thái Ψ ban đầu bị phá hủy vì sau các phép đo, Ψ co lại thành hoặc trạng thái 0 hoặc 1 tùy theo kết quả đo được đối với qubit số 1 (hình 2). Hiện tượng này gọi là định lý “không nhân bản được” (no-cloning theorem).
Mật mã lượng tử (Quantum cryptography)
Mật mã là khoa học trao đổi thông tin dưới dạng mã hóa mà người ngoài cuộc (trừ người gửi và người nhận) không phá mã được. Đây là một vấn đề lớn phức tạp.
Một tin mã hóa có nghĩa là một tin mà chỉ riêng người gửi và người nhận biết được mà thôi. Ví dụ một tin M có thể mã hóa qua E nhờ thuật toán sau: E = Ms mod c.
Nếu c là tích của hai số nguyên tố p & q thì người ta có thể chứng minh rằng M có thể bẻ khóa được theo thuật toán: M = E t mod c.
Trong đó t là một hàm số đơn giản của p&q. Chỉ cần giữ bí mật p&q, các đại lượng khác có thể cho biết công khai. Nếu c đủ lớn thì bẻ khóa bằng cách tìm p&q là một việc không làm nổi đối với máy tính cổ điển hiện dùng.
Mã RSA (Rivest,Shamir& Adleman) sử dụng ý tưởng trên. Đây là bài toán thừa số hóa (factorization), song hiện nay sử dụng thuật toán Shor người ta có hy vọng bẻ được khóa.
Chỉ có cách dùng mật mã lượng tử (quantum cryptography) mới tránh được bẻ khóa khi phát giác được kẻ nghe trộm (eavesdropper).
Biên bản (protocol) BB84 (C.H.Bennett&G. Brassard, 1984)[2] (từ biên bản ở đây có nghĩa là phương thức hiệp đồng).
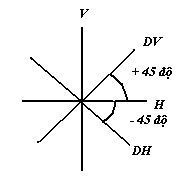
Alice dùng hai kiểu phân cực (polarization settings) A và B, xem hình 3:
1/ A: dọc và ngang
2/ B: chéo – 45 độ và + chéo + 45 độ
Alice bắt đầu với 4n qbit. Mỗi qbit có 4 trạng thái: [0 ,1] và [-,+]. Hai trạng thái đầu ứng với kiểu phân cực A của bit 0 và bit 1, tương tự như vậy hai trạng thái sau ứng với kiểu B.
Ta có 3 nhân vật: Alice (người gửi thông điệp về khóa), Bob (người nhận) & Eve (điệp viên=eavesdropper=nghe trộm) [3].
Alice gửi đi khóa mật mã bằng cách dùng các bit 0 & 1.
 |
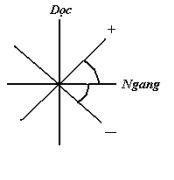 |
Hình 3. Các kiểu phân cực A (dọc, ngang) và B( -,+)
Ví dụ: Alice gửi đi bit 0 trong kiểu phân cực A vậy photon có phân cực dọc.
Bob khi nhận thông điệp này không biết được kiểu phân cực mà Alice đã dùng cho nên phải chọn một kiểu phân cực bất kỳ, ví dụ Bob chọn đúng kiểu A mà Alice đã dùng và thu được photon phân cực dọc tức bit 0. Vậy mọi việc đều ổn.
Song nếu Bob lại chọn kiểu phân cực B (tức khác với kiểu phân cực A mà Alice đã dùng khi gửi thông điệp) thì 50% Bob chọn là photon phân cực – tức bit 0 và 50% photon phân cực + tức bit 1.
Bây giờ nếu có một kẻ nghe trộm là Eve. Sau khi Alice gửi thông điệp đi Eve nghe trộm và lẽ dĩ nhiên Eve cũng không biết kiểu phân cực mà Alice đã dùng nên chọn một kiểu phân cực bất kỳ. Nếu Eve chọn A thì thu được bit 0 và gửi tiếp cho Bob thông điệp của Alice cho Bob và không có điều gì xảy ra. Song nếu Eve chọn sai kiểu phân cực ví dụ Eve chọn B thì 50% Eve sẽ gửi cho Bob bit 1. Và Bob sẽ thu được kết quả sai, mặc dầu Bob đã chọn đúng kiểu phân cực A mà Alice đã dùng. Như thế có nghĩa là dẫu cho Alice và Bob đều chọn chung một kiểu phân cực là A họ vẫn không thu được kết quả đúng nếu trên quá trình có kẻ nghe trộm.
Sau mọi việc kết thúc Alice báo cho Bob (bằng phương tiện công cộng) dãy các kiểu phân cực mình đã sử dụng. Alice và Bob chọn những trường hợp kết quả trùng nhau. Chú ý dãy các kiểu phân cực không làm lộ tý nào thông điệp về khóa.
Để có thống kê đủ bảo đảm độ chính xác Alice và Bob có thể chỉ lấy 2n bit trong kết quả của họ. Alice chọn n bit nào đó và báo cho Bob biết. Alice & Bob so sánh các kết quả. Nếu có hơn t bit không trùng nhau thì họ hủy bỏ tất cả quá trình đã thực hiện và đổi khóa. Nếu chọn t sao cho thí nghiệm được xem là chấp nhận được thì họ thỏa thuận nhau và có được m bit khóa mật mã từ số n bit còn lại.
Biên bản EPR [2] & [3]
Trong biên bản BB84 ta thấy dường như mọi việc xuất phát từ Alice. Song khóa có thể phát sinh từ quá trình gắn liền với liên đới lượng tử. Điều này sẽ được thấy từ biên bản sau đây.
Trong biên bản EPR Alice (hoặc nhờ một đối tác thứ 3 nào đó) có thể chuẩn bị những cặp EPR rồi giữ lại một hạt còn hạt kia gửi cho Bob. Từ lúc này thì quá trình ở đây là đối xứng đối với Alice và Bob. Những cặp EPR mô tả nội dung của key mật mã. Tiếp theo đó Alice chuẩn bị một dãy polarization settings (b) rồi đo hạt EPR của mình và thu kết quả (a) còn Bob tương tự như vậy cũng đo hạt EPR của Bob trong một polarization settings mà Bob tạo ra (b’) và thu kết quả (a’).
Sau đó Alice & Bob dùng phương tiện công cộng trao đổi nhau (b) và (b’) và chỉ giữ lại những kết quả lúc b = b’ và ta trở về trường hợp biên bản BB84.
Kết luận
Thái độ không tin tưởng vào cơ học lượng tử của Einstein lại dẫn đến những phát hiện quan trọng để hiểu CHLT thêm sâu sắc và người ta cũng không ngờ rằng những điều kỳ lạ của CHLT lại là những điều kỳ diệu cho công nghệ tin học & thông tin hiện đại. Theo hãng thông tấn Thomson Reuters (Mỹ) ba nhà vật lý: Alain Aspect (Pháp), John F. Clauser (Mỹ), Anton Zeilinger (Áo) nghiên cứu liên đới lượng tử đã nằm trong danh sách dự báo giải Nobel 2011, vì vấn đề nghiên cứu này vừa là một vấn đề cơ bản của CHLT lại vừa liên quan đến công nghệ tin học cho nên nhiều người tin rằng ba nhà vật lý trên có hy vọng đoạt giải này trong tương lai.
——————-
Tài liệu tham khảo
[1] Zeeya Merali, Le test ultime de la mecanique quantique, La recherche No 455 tháng 09/2011.
[2] Michael A.Nielsen & Isaac L.Chuang, Quantum Computation and Quantum Information, Cambridge, University Press.
[3] Toney Hey & Patrick Walters, The new quantum universe, Cambridge, 2003.
