Euler người thầy vĩ đại: Một số đóng góp tiêu biểu
Trong hai kỳ trước chúng ta đã tìm hiểu cuộc sống thăng trầm và các đóng góp cơ bản của Euler, kỳ này Tia Sáng giới thiệu tới bạn đọc một số đóng góp tiêu biểu của Euler, nội dung sẽ bao gồm nhiều kiến thức Toán học.
Euler với lý thuyết số
Số hoàn hảo
Ngay từ thời của Pythagoras (thế kỷ thứ 6 trước Công nguyên) câu hỏi đặt ra với các số hoàn hảo đã được biết tới.
Định nghĩa số hoàn hảo: Số hoàn hảo là một số nguyên dương mà tổng các ước thực sự của nó bằng chính nó.
Ví dụ: Các ước thực sự của 6 là 1,2,3 và 6=1+2+3.
Trong quá trình nghiên cứu về số hoàn hảo, Euler đã đưa ra một số khái niệm và các khái niệm này đều có những đóng góp to lớn không chỉ cho riêng việc nghiên cứu các số hoàn hảo.
Định nghĩa: σ (n) là tổng các ước nguyên dương của n. (Ban đầu Euler sử dụng kí hiệu ∫(n), ngày nay kí hiệu đó được sử dụng cho tích phân.)
Euler cũng đưa chứng minh nhiều khẳng định liên quan tới σ (n).
Mệnh đề: Nếu n là một số hoàn hảo thì σ (n) = 2n.
Định lý: Nếu n là một số hoàn hảo chẵn thì n = 2k-1 (2k-1) và 2k -1 là một số nguyên tố.
Với định lý nêu trên, Euler đã chỉ ra dạng của các số hoàn hảo chẵn, nhưng như vậy vẫn là chưa đủ cho bộ óc vĩ đại của mình, năm 1747 trong một bài báo của mình, Euler đã đưa ra câu hỏi “Liệu có số hoàn hảo nào là số lẻ?” Sau đó, ông gọi đó là vấn đề khó nhất. Vào thời điểm đó tất cả mọi người đều tin rằng đó là một vấn đề thực sự khó, vì ngay cả Euler cũng xác nhận điều đó.
Cho đến ngày nay, vấn đề về sự tồn tại của một số hoàn hảo lẻ vẫn còn là một thách thức cho tất cả các nhà toán học. Họ vẫn chưa thể khẳng định được sự tồn tại của số hoàn hảo lẻ. Ngay cả với sự trợ giúp của các hệ thống siêu máy tính thì câu hỏi trên vẫn là một câu hỏi mở. Có rất nhiều người đã tham gia nghiên cứu vấn đề này và cũng cho ra nhiều kết quả thú vị.
* Một số hoàn hảo lẻ không thể chia hết cho 105.
* Số hoàn hảo lẻ nhỏ nhất lớn hơn 10300
* Một số hoàn hảo lẻ có ít nhất ba thừa số nguyên tố khác nhau.
* Tổng nghịch đảo của các số hoàn hảo lẻ là hữu hạn. ![]()
Đây là một điều rất thú vị bởi trong giải tích thì ![]() không hội tụ, nhưng nếu chỉ lấy trên tập các số hoàn hảo lẻ thì nó lại hữu hạn.
không hội tụ, nhưng nếu chỉ lấy trên tập các số hoàn hảo lẻ thì nó lại hữu hạn.
Hi vọng trong tương lai gần các nhà Toán học sẽ có câu trả lời cho vấn đề “số hoàn hảo lẻ”.
Số nguyên tố và hàm Zeta
Bắt đầu với bài toán Basel tính tổng nghịch đảo các bình phương
![]()
Tổng quát hoá tổng trên ta được hàm Zeta ![]()
Euler đã tính được ![]() bằng cách xét đa thức
bằng cách xét đa thức
![]()
sau đó Euler viết P(x) dưới 2 dạng khác nhau và đồng nhất hệ số để tính được ζ (2).
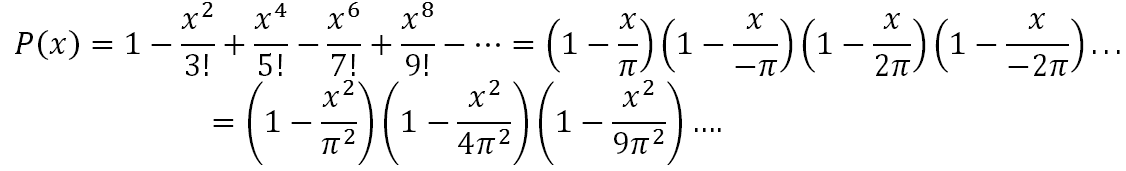
Xét hệ số của x2 trong P(x) nói trên, ta có:
![]()
Và cuối cùng thu được ![]()
Không dừng lại ở đó, Euler còn tính được kết quả tổng quát .
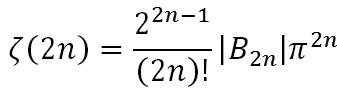
Trong đó |B2n| là số Bernoulli
Euler gặp khó khăn với trường hợp s lẻ và ông không tin nó có liên quan tới ![]() . Ngày nay thì đây cũng là một câu hỏi mở đang chờ được các nhà toán học giải đáp.
. Ngày nay thì đây cũng là một câu hỏi mở đang chờ được các nhà toán học giải đáp.
Trong quá trình tính toán với các bài toán trên, Euler đã đưa ra rất nhiều đẳng thức bất ngờ và nhiều điểm độc đáo, sau này trở thành các công cụ tính toán mạnh cho nhiều nhà toán học. Với lý thuyết số, Euler còn chứng minh rất nhiều định lý quan trọng trong lý thuyết đồng dư, số nguyên tố, số Mersenne… do khuôn khổ bài viết nên tôi chỉ trình bày sơ lược các kết quả đại diện trong các lĩnh vực mà Euler để lại.
Euler và định lý cơ bản của đại số
Định lý: Mọi đa thức bậc n với hệ số phức luôn phân tích được thành n nhân tử tuyến tính
Đây là định lý cơ bản của đại số, một trong những định lý quan trọng nhất và được sử dụng rộng rãi không chỉ riêng trong đại số. Các chứng minh của định lý này cho đến nay vẫn chưa có một chứng minh nào là thuần tuý đại số, các chứng minh đã có đều mang chút ít màu sắc của giải tích phức.
Năm 1794, Euler cũng đưa ra một phác thảo chứng minh cho định lý cơ bản của đại số. khi đó Euler mới chỉ cụ thể hoá được trường hợp bậc 4.
Định lý Euler-Fermat và Mật mã
Định lý: Nếu a và n là hai số nguyên tố cùng nhau thì aφ(n) ≡ 1 (mod n). Với φ(n) là phi hàm Euler.
Trong mật mã, ta quan tâm tới việc truyền thông tin một cách an toàn từ người gửi tới người nhận. Một thông điệp M được mã hoá thành E và người nhận sẽ giải mã từ E thu được M. Sẽ rất thuận tiện nếu mỗi kí tự trong bảng mã ASCII được thay thế bằng các số tự nhiên, khi đó việc biến M → E sẽ chuyển sang ngôn ngữ ánh xạ f : N → N. Vấn đề ta phải tìm một hàm f thoả mãn:
– f là một song ánh
– f có công thức và khó tìm được nghịch ảnh của f.
Một giải pháp cho vấn đề này là chương trình mã hóa RSA đang được sử dụng rộng rãi (đặt theo tên nhà phát minh của nó R. Rivet, A. Shamir và Adleman L.)
Tạo Mã và Mã hoá
* Chọn hai số nguyên tố p,q lớn và khác nhau.
* Tính n = p.q
* Tính giá trị của φ(n) = (p-1) (q-1)
* Chọn 1 số nguyên tố e thoả mãn: 1<e<φ(n) và e nguyên tố cùng nhau với φ(n).
* Tìm d: (d.e) ≡ 1 mod (φ(n))
Mã công khai là n, module và e số mũ công khai, mã bí mật
![]()
Người gửi chuyển thông tin M thành số m<n theo một hàm chuyển đổi. Lúc này cả người gửi và người nhận đều có m và n, người nhận tìm c là bản mã hoá của n: c = m2 mod (n)
Bánh răng Euler
 |
Trong quá trình làm việc với thiết kế tua bin nước, Euler đã tối ưu cho các bánh răng để giảm sức lao động, giảm tiếng ồn… Euler không chỉ là người phát minh ra mà còn dự đoán được cả quỹ đạo chuyển động của nó. Bánh răng này được gọi là bánh răng – Euler. Sau này người ta còn gọi đó là phương trình Euler–Savary.
Đĩa Euler
Euler cũng nghiên cứu tới chuyện động của các vật thể xoay quanh một trục, có tính tới ma sát. Một ví dụ thú vị là đĩa Euler, một đĩa tròn (đồng nhất) bằng kim loại được quay trên một bề mặt mịn sạch. Lúc đầu, nó sẽ xoay xung quanh trục thẳng đứng của nó, nhưng do ma sát, trục đang bắt đầu nghiêng và đĩa để cuộn trên một đường tròn. Càng ngày trục nghiêng càng bị nghiêng dần, các vòng tròn thì ngày một rộng ra. Dù có xét đến yếu tố nào đi nữa thì quả bóng vẫn sẽ dừng lại.
 |
Chìa khóa để giải thích chuyển động này là phương trình Euler, một tập hợp các phương trình vi phân liên quan đến các góc Euler và các thông số khác. Các chi tiết kỹ thuật của các chuyển động, vẫn còn được tiếp tục nghiên cứu cho tới tận bây giờ.
Lý thuyết đồ thị và Tôpô
Con sông Pregel, chảy qua thành phố Phổ Königsberg, chia thành phố thành một hòn đảo và ba vùng đất riêng biệt, một ở phía Bắc, một ở phía Đông, và một ở phía Nam. Có tất cả bảy cây cầu, sắp xếp như trong bản đồ với các điểm màu xanh lá cây.
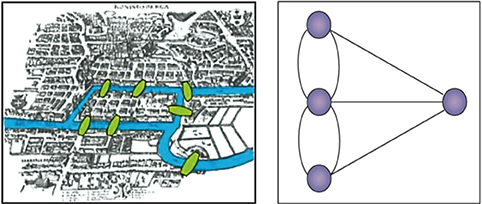 |
Bài toán: người ta có thể đi dạo từ một điểm ở thành phố khác bằng cách đi qua mỗi cây cầu đúng một lần? Bậc của một đỉnh là cạnh nối với nó; trong đồ thị các cây cầu Königsberg, ba nút có bậc bằng 3 và một nút có bậc 5. Euler đã chứng minh rằng một chu trình có dạng như mong muốn chỉ tồn tại khi và chỉ khi không có nút bậc lẻ. Một đường đi như vậy được gọi là một chu trình Euler. Do đồ thị các cây cầu Königsberg có bốn nút bậc lẻ, nên nó không thể có chu trình Euler.
Lời giải của Euler cho bài toán trên là cơ sở cho nền móng của Topo học. (Xem thêm bài viết của Nguyễn Hữu Việt Hưng trên Tia Sáng số 6 – 20/3/2016.)
Công thức Euler
Với mọi số thực x ta luôn có: eix = cos x + i.sin x . Với e là số vô tỉ được tính qua giới hạn
![]()
công thức Euler là phổ biến trong toán học, vật lý và kỹ thuật. Nhà vật lý Richard Feynman được gọi là phương trình “viên ngọc quý” và “công thức đáng chú ý nhất trong toán học.”
Một công thức tương đương là ix= ln (cos x + i sin x), công thức này được đưa ra bởi Cotes (1714). Công thức Euler được sử dụng trong rất nhiều lĩnh vực của Toán từ lý thuyết số phức, phương trình vi phân,…từ đơn giản nhất cho đến phức tạp.
Qua ba bài viết, chúng ta đã cùng có một hành trình xuyên suốt cuộc đời và sự nghiệp của nhà Toán học vĩ đại Euler, một người thầy vĩ đại bởi tất cả những gì ông để lại đã trực tiếp hoặc gián tiếp tạo nên bộ mặt khoa học và cuộc sống ngày nay.
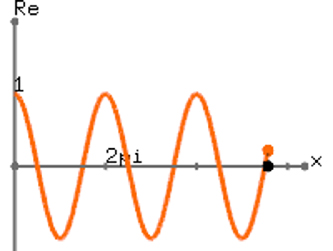 Đồ thị phần thực của eix. |
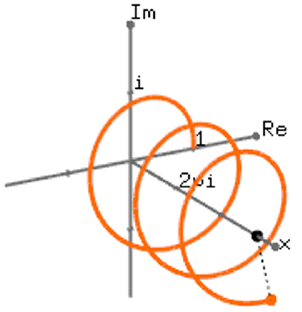 Đồ thị của eix |
