Hấp dẫn, điện và từ học trong trái tim vật lý hiện đại
Cách đây không lâu, nhân sự kiện phát hiện sóng hấp dẫn, Viện Hàn lâm Khoa học và Công nghệ Việt Nam (VAST) đã tổ chức một buổi nói chuyện thảo luận về chủ đề này. Tại buổi nói chuyện, một nhà vật lý có nhiều kinh nghiệm đã đặt ra một câu hỏi: tại sao trọng lực lại là lực tensor (hay chính xác hơn tại sao hạt truyền tương tác hấp dẫn - graviton - lại có spin 2). Vì không có ai trong hội trường đưa ra câu trả lời thỏa đáng cho câu hỏi này nên tôi nghĩ đây có thể là chủ đề thú vị cho một bài báo trên Tia Sáng. Những dòng tôi viết dưới đây với mục đích bình luận về sự phong phú và sâu sắc của vật lý ẩn đằng sau câu hỏi tưởng chừng như đơn giản này. Tôi sẽ cố gắng sử dụng ngôn ngữ đơn giản mà người đọc có thể hiểu được. Bài viết không phải là một bài giảng mà chỉ đơn giản hy vọng kích thích trí tò mò của người đọc.
Graviton là một hạt cơ bản, giả thuyết có vai trò là hạt trao đổi của lực hấp dẫn trong khuôn khổ lý thuyết trường lượng tử. Nếu nó tồn tại, Graviton dự kiến sẽ không có khối lượng hoặc rất nhỏ (vì lực hấp dẫn xuất hiện với phạm vi không giới hạn) và phải có spin là 2.
Chúng ta đã học ở phổ thông trung học rằng hai điện tích, q và q’, hút hoặc đẩy nhau bởi lực Coulomb có độ lớn tỉ lệ với qq’/r2 và hai vật có khối lượng, m và m’, hút nhau bởi lực Newton có độ lớn tỉ lệ với mm’/r2, ở đó r là khoảng cách giữa hai điện tích và hai trọng vật. Vẻ tương tự bề ngoài của hai định luật này có thể khiến ta nghĩ (một cách sai lầm!) rằng hai tương tác này có bản chất giống nhau. Tuy nhiên, trên thực tế chúng lại rất khác nhau như được minh họa ở phần tiếp theo. Trong bài báo này, tôi sẽ cố gắng bỏ qua những kiến thức về vật lý lượng tử và thuyết tương đối và chỉ sử dụng kiến thức vật lý cổ điển.
Lực Coulomb và Newton: lực tầm xa
Ta có thể nhận ra điểm chung giữa lực Coulomb và Newton là độ lớn của chúng tỉ lệ nghịch với bình phương khoảng cách giữa hai điện tích điểm hoặc hai chất điểm. Điều này có nghĩa là các lực này không bao giờ bằng không, thậm chí ở những khoảng cách rất lớn. Thực vậy, đó là một đặc điểm hết sức quan trọng của trọng lực: trọng lực trên Trái đất là tổng hợp sức hút của tất cả vật chất trên hành tinh này; đó là một lực có độ lớn đáng kể mặc dù cường độ của lực hấp dẫn bị giới hạn bởi hằng số hấp dẫn (hằng số Newton G) có giá trị rất nhỏ; thể tích khổng lồ của Trái đất đã bù đắp cho cường độ nhỏ của trọng lực. Tuy nhiên, lực Coulomb lại không giống như vậy. Nếu ta có một tập hợp những điện tích điểm tích điện cùng dấu, chúng sẽ ngay lập tức đẩy nhau và rất khó để có thể giữ chúng lại với nhau trong một thể tích xác định được. Vật chất thông thường được cấu tạo bởi các hạt mang điện tích dương và âm, tương ứng với hạt nhân và các electron. Với tập hợp các hạt tích điện như vậy, bất kỳ một thể tích vĩ mô nào về cơ bản cũng đều trung hòa về điện và do đó không tạo ra lực đáng kể ở khoảng cách lớn: các điện tích chắn lẫn nhau, hay còn gọi là hiệu ứng chắn Debye. Tách các điện tích dương khỏi các điện tích âm trong một tập hợp như vậy là rất khó và đó là chủ đề cơ bản của vật lý plasma: hệ điện tích sẽ ngay lập tức chống lại ngoại lực bởi những chuyển động theo hướng tái thiết lập tính trung hòa của nó, tạo nên sóng lan truyền trong plasma như sóng Alfven. Tuy nhiên, lực Coulomb lớn hơn lực hấp dẫn Newton nhiều lần, lên đến 1039 lần, do đó nhiều hiệu ứng thú vị có thể được quan sát với lực Coulomb: ví dụ, thí nghiệm Millikan đo hiệu ứng khi thêm một điện tử lên trên bề mặt một giọt dầu trung hòa về điện, ở đó các nguyên tử của giọt dầu chứa khoảng 1015 electron; một ví dụ khác về giới hạn trên tốt nhất về khối lượng của photon, 10-60 g, thu được từ thực nghiệm giả thuyết lực hấp dẫn và lực điện từ của Đám mây Magellan Nhỏ cân bằng với nhau.
Khi dùng vật lý lượng tử để mô tả lực điện và lực hấp dẫn, sự phụ thuộc của chúng vào 1/r2 có nghĩa là những hạt truyền tương tác tương ứng, photon và graviton, phải là những hạt không có khối lượng. Ta thấy rõ rằng, hai lực này phụ thuộc vào 1/r2 do đó tồn tại một điểm kỳ dị tại r=0 khi đó các lực này trở nên lớn vô hạn, không có ý nghĩa vật lý: chúng ta cần phải điều chỉnh lý thuyết để mô tả trường hợp này. Tôi sẽ bình luận về điểm này trong phần sau của bài báo.
Hấp dẫn và nguyên tắc Mach
Một điều đặc biệt của hấp dẫn là: khối lượng “động lực” m trong định luật Newton (F=mM/r2) lại chính xác bằng khối lượng “quán tính” (m trong K=1/2mv2, ở đó K là động năng và v vận tốc của vật). Điều này làm cho trọng lực rất khác so với các lực khác: trong cùng một trường, chẳng hạn như trọng trường của Trái đất, tất cả các trọng vật đều rơi như nhau bất kể giá trị khối lượng của chúng là bao nhiêu. Điều này lần đầu tiên được Galileo chứng minh với thí nghiệm tháp nghiên Pisa nổi tiếng của ông. Đặc điểm này gợi nên việc xem hấp dẫn như là sự biến dạng của không gian do trọng vật nằm trong đó gây ra, khác biệt với các loại lực khác như lực Coulomb. Cách tiếp cận này chính là ở cơ sở của thuyết tương đối tổng quát và nó giúp giải quyết một vấn đề đã làm đau đầu nhiều nhà vật lý trong nhiều thế kỷ: không gian vẫn vậy với những gì nó chứa đựng hay những thứ mà không gian chứa đựng mới đem lại ý nghĩa cho nó? Hay câu hỏi cũng có thể được đặt như sau: Không gian là tuyệt đối hay tương đối? Nhiều triết gia và nhà khoa học đã thảo luận về câu hỏi này trong nhiều thế kỷ qua, trong số đó có thể kể đến Democritos, Aristotle, Plato, Descartes, Leibniz, Newton, Huygens, Berkeley, Kant và Euler. Khi quan sát thấy hình dạng bề mặt của mặt nước trong một cái xô đứng yên và một cái chuyển động quay khác nhau, Newton đã đưa ra khái niệm chuyển động tuyệt đối: sự quay so với không gian tuyệt đối là nguyên nhân của sự khác biệt. Quan điểm về không gian tuyệt đối gặp phải nhiều phê phán, nổi tiếng nhất là phê phán do Mach đưa ra. Những phân tích của ông về vấn đề này có ảnh hưởng lớn tới Einstein, người gọi công trình của Mach là Nguyên lý Mach. Mach khẳng định rằng chuyển động tuyệt đối và không gian tuyệt đối chỉ là sản phẩm của trí não, không thể kiểm chứng được bằng thực nghiệm, do vậy, đó là những khái niệm siêu hình vô nghĩa và không nên được sử dụng trong khoa học. Ông nói, tất cả các định luật của cơ học đều dựa vào cảm nhận về vị trí và chuyển động tương đối và chúng ta không được phép sử dụng các định luật này ngoài giới hạn của chúng. Con lắc Foucault dao động trong mặt phẳng cố định đối với các ngôi sao mà không bị ảnh hưởng bởi sự quay của Trái đất là bằng chứng cho hệ quy chiếu gắn với toàn bộ Vũ trụ. Bài viết này sẽ không thảo luận sâu hơn nữa về điểm này, những thảo luận sâu hơn có thể tìm thấy trong tài liệu tham khảo sau đây: Herbert Lichtenegger và Bahram Mashhoon, Phép đo Điện-Từ-Hấp dẫn: Một công việc đầy thách thức, ed. L. Iorio, Nova Science, New York, 2007, arXiv: vật lý / 0.407.078.
Điện và Từ: lực vector
Điểm đặc biệt của lực Coulomb là nó luôn được xem xét cùng với lực từ. Một điện tích chuyển động sẽ tạo ra từ trường và, ngược lại, trường từ tác động lực lên điện tích chuyển động. Hai dây dẫn song song mang theo hai dòng điện chạy cùng hướng sẽ hút nhau. Đây là kết quả của trường từ sinh ra bởi dòng điện của dây này tại vị trí của dây kia. Chú ý rằng cường độ lực từ trong ví dụ này nhỏ hơn rất nhiều so với lực Coulomb mà các electron chuyển động trong hai dây dẫn có thể đẩy nhau; tuy nhiên, do hiệu ứng chắn đề cập ở phần trên (dây điện được làm bằng vật chất trung hòa về điện vì vậy lực đẩy rất lớn giữa các electron mang điện tích âm trong hai dây cơ bản bị triệt tiêu) nên lực từ, không bị tác động bởi hiệu ứng chắn, trở thành lực áp đảo. Vì sự liên hệ sâu sắc giữa điện và từ nên lý thuyết về tương tác điện từ hiện đại mô tả lực từ là sự điều chỉnh tương đối tính của lực Coulomb, bình luận sâu hơn về điều này vượt ra ngoài phạm vi của bài viết này. Ở đây, đủ để nói rằng, điện từ đơn giản được mô tả dưới dạng một trường điện E và trường từ B và lực tác động lên một điện tích q chuyển với vận tốc v là F=q(E+v×B). Sự biến đổi của E và B khi chuyển hệ quy chiếu được mô tả một cách đẹp đẽ là một tensor bậc 4, được gọi là tensor điện từ, bản thân nó có thể được viết dưới dạng đạo hàm không và thời gian của một vector bốn chiều. Thế năng điện từ bao gồm thế năng điện (đại lượng vô hướng, thành phần thời gian) và thế năng từ (đại lượng vector, thành phần không gian). Hình thức luận này cho phép ta viết toàn bộ lý thuyết điện từ (các phương trình Maxwell) dưới dạng hết sức đơn giản và nó khiến cho bản chất vector của tương tác điện từ trở nên rõ ràng và do đó lượng tử truyền tương tác, photon, của trường điện từ có spin bằng 1.
Trọng lực: lực tensor
Rõ ràng lực hấp dẫn Newton và lực Coulomb có bản chất rất khác nhau: tất cả các trọng vật đều “dương” trong khi điện tích có thể mang điện tích âm hoặc dương. Hơn nữa, một trọng vật chuyển động không tạo ra trường tương đương với trường từ. Với các điện tích cùng dấu, lực Coulomb là đẩy trong khi lực Newton luôn là lực hút. Cũng có giả thuyết cho rằng có thể tồn tại các hạt có khối lượng âm, đặc biệt là phản hạt, có thể bị đẩy hấp dẫn bởi các hạt thông thường. Tuy vậy, ta có thể bỏ qua những giả thuyết này một cách an toàn vì cho đến nay chưa có bằng chứng thực nghiệm nào ủng hộ sự tồn tại của chúng.
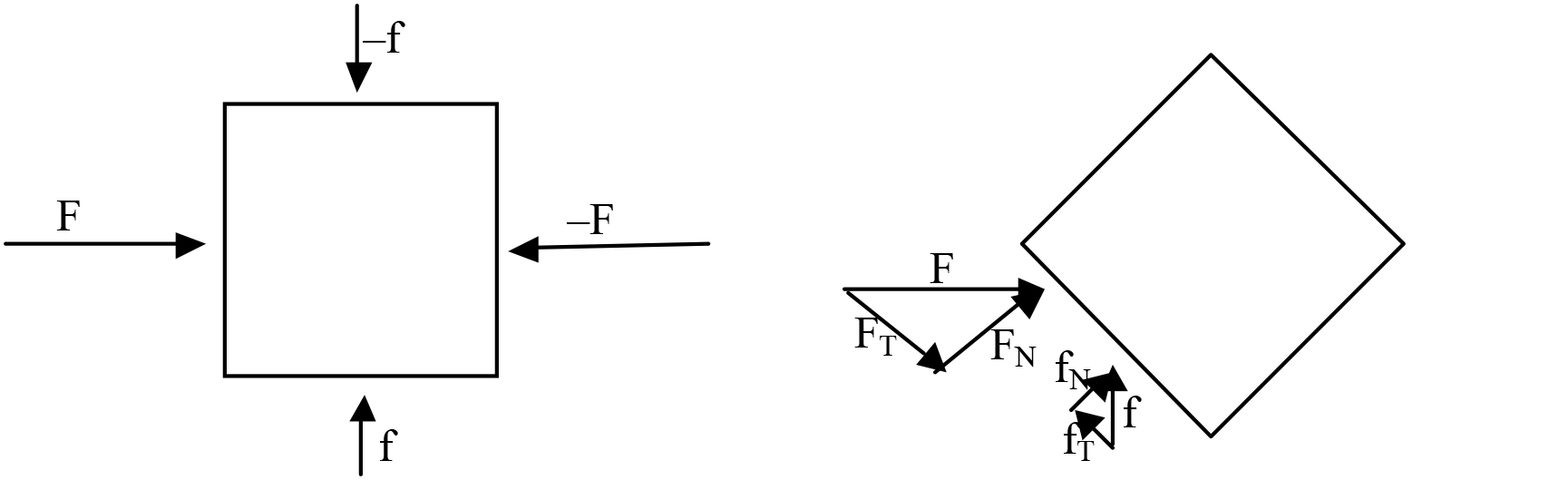
Để hiểu rõ hơn bản chất của trọng lực, chúng ta cần phải hiểu tác động của nó lên vật chất như thế nào. Như những nhận xét bên trên, là lực phụ thuộc vào khoảng cách nên để phân tích tương tác giữa hai chất điểm chúng ta không thể không đối mặt với thuyết tương đối hẹp khi vận tốc của chúng đạt tới vận tốc gần với vận tốc ánh sáng ở khoảng cách ngắn và phải đối mặt với vật lý lượng tử ở khoảng cách rất ngắn. Cách tiếp cận của Einstein để tránh những khó khăn này là phân tích tác động của hấp dẫn lên môi trường liên tục, đặc biệt tác động của trường hấp dẫn do chính những vật này tạo ra. Khi làm như vậy, chúng ta đã giấu rác dưới thảm với ngầm định rằng một số lực nào đó mà ta không nói đến đã ngăn cản vật chất suy sụp dưới sức nặng của nó. Do đó, chúng ta phải chấp nhận hạn chế tham vọng của mình với việc sử dụng lý thuyết hấp dẫn được xấp xỉ ở khoảng cách lớn. Khi đó các lực hoặc ứng suất có mặt ở mọi nơi trong môi trường liên tục có thể được mô tả bởi một tensor T bậc 3, được gọi là tensor ứng suất, lần đầu tiên được giới thiệu bởi Cauchy. Ý tưởng cơ bản là: tại bất kỳ điểm nào trong môi trường, các thành phần của lực F tác động lên một bề mặt nhỏ, có vector pháp tuyến n , phụ thuộc tuyến tính vào các thành phần của n. Điều này có thể được viết đơn giản như sau dF=n.T, ở đó T là tensor có 3×3=9 thành phần. Tuy nhiên, vì lực tác dụng theo hướng của n bằng về biên độ và ngược hướng với lực tác dụng theo hướng -n, do đó số thành phần của tensor T giảm xuống chỉ còn là 6. Đây là ba góc xác định hướng của hệ quy chiếu trong đó ma trận biểu diễn tensor được chéo hóa và ba ứng suất nén dọc theo mỗi trục của hệ quy chiếu này (các giá trị bên ngoài đường chéo tương ứng với ứng suất biến dạng). Đặc biệt, trong thủy tĩnh học, ba ứng suất nén này đều bằng nhau và ngược hướng với áp lực hiện diện trong chất lỏng.
Như vậy, ý tưởng cơ bản của thuyết tương đối tổng quát: lực hấp dẫn được mô tả là sự biến dạng của không gian do trọng vật hiện diện trong đó gây ra. Do đó, ý tưởng này đòi hỏi phải xây dựng mối liên hệ giữa những biến dạng không gian với tensor ứng suất. Chúng ta học được từ hình học vi phân rằng biến dạng địa phương của không gian cũng được mô tả bởi một tensor, do đó có thể phát biểu rằng tensor ứng suất và tensor biến dạng đơn giản tỷ lệ với nhau, đây chính là ý nghĩa của phương trình thuyết tương đối rộng của Einstein.
Một vài bình luận thêm về điều này là cần thiết: thứ nhất, chúng ta không nên quên rằng thuyết tương đối tổng quát, như đã nói, chỉ là một xấp xỉ ở khoảng cách lớn của thuyết hấp dẫn; thứ hai, thuyết tương đối hẹp lặp lại những lập luận trên nhưng cho không-thời gian, với tensor bậc 4; thứ ba, theo truyền thống thuyết tương đối tổng quát thường được dạy sau thuyết tương đối hẹp với lý do là Einstein phát minh ra thuyết tương đối hẹp trước thuyết tương đối rộng; nhưng theo tôi chúng ta không đúng khi làm như vậy: những ý tưởng cơ bản của thuyết tương đối tổng quát mà tôi phác thảo bên trên dường như tự nhiên và dễ hiểu hơn nhiều so với ý tưởng cơ bản của thuyết tương đối hẹp, một lý thuyết chứa đựng nhiều khái niệm đi ngược với nhận thức chung của chúng ta.
Tôi hy vọng đến đây bản chất tensor của lực hấp dẫn đã trở nên rõ ràng với đọc giả.
Giới thiệu về thuyết tương đối và thuyết lượng tử
Mở rộng những phát triển trên với thuyết tương đối hẹp là rõ ràng, nó không làm phức tạp thêm vấn đề thậm chí còn làm cho lý thuyết trở nên đơn giản và đẹp hơn. Điều này đặc biệt đúng đối với trường hợp điện từ; những sự phức tạp ban đầu được đưa vào lý thuyết bởi những người tiên phong, chẳng hạn như việc đưa vào thế trễ không còn cần thiết khi lý thuyết được xem xét trong khuôn khổ thuyết tương đối hẹp. Khi mô tả lượng tử lý thuyết này, sóng điện từ lan truyền với vận tốc của ánh sáng, xuất hiện như là đối tượng truyền tương tác giữa các hạt tích điện và dẫn đến việc đưa vào một vector có spin bằng 1, photon.Với hợp của trọng lực, sự ra đời của thuyết tương đối hẹp cũng làm đẹp thêm những luận cứ phát triển trong phần trước. Tensor ứng suất và biến dạng bây giờ được mở rộng cho bốn chiều không-thời gian; tensor ứng suất trở thành tensor ứng suất-năng lượng; còn tensor biến dạng chính là tensor Ricci mô tả sự biến dạng của không-thời gian. Phương trình Einstein chỉ đơn giản là sự biểu diễn tương quan giữa hai tensor bậc 4 này.Tuy nhiên, khi đưa các hiệu ứng lượng tử vào thuyết hấp dẫn (lượng tử hóa thuyết hấp dẫn), ta gặp phải những khó khăn rất cơ bản. Nói đại khái, hệ thức bất định Heisenberg không cho phép tích của khối lượng với kích thước của một vật nhỏ hơn một giá trị xác định (bằng hằng số Planck). Vì vậy, khi thể tích của vật trở nên rất nhỏ, khối lượng của nó không thể nhỏ hơn một giá trị xác định và do đó lực Newton trong vật cũng không thể nhỏ hơn. Tại khoảng cách rất nhỏ, gọi là thang Planck, cỡ khoảng 10-33 cm, lực Newton tăng nhanh hơn so với sự suy giảm kích thước, và trở thành quá lớn đối với các kích thước của vật, làm cho thuyết lượng tử và thuyết hấp dẫn trở nên không còn tương thích với nhau (nhớ rằng điều này xảy ra vì lực Newton tỉ lệ nghịch với bình phương khoảng cách, khi khoảng cách rất nhỏ lực trở nên rất lớn). Vấn đề này là một trong những vấn đề chính của vật lý hiện đại ngày nay. Do đó, nói đúng ra, hiện tại nói về graviton là vô nghĩa (graviton là hạt truyền tương tác hấp dẫn trong thuyết hấp dẫn lượng tử). Tuy nhiên, thực tế, người ta có thể viết nên một lý thuyết hấp dẫn lượng tử gần đúng và thuyết phục chính mình rằng năng lượng phát ra bởi tương tác hấp dẫn có dạng sóng, được gọi là sóng hấp dẫn. Bản chất tensor của hấp dẫn ngụ ý rằng những sóng như vậy gây ra biến dạng (tứ cực) tensor khi truyền qua vật chất, và phải được liên kết với graviton có spin bằng 2 trong biểu diễn lượng tử của nó. Cho đến gần đây, ta mới thu được bằng chứng về sóng hấp dẫn một cách gián tiếp: nhờ phép đo suy giảm năng lượng rất nhỏ của hệ pulsar đôi năm 1974, công trình được trao giải thưởng Nobel cho hai nhà khoa học Hulse và Taylor. Mới gần đây, sóng hấp dẫn phát ra bởi sự và chạm và hòa nhập của hai lỗ đen đã được phát hiện lần đầu tiên một cách trực tiếp.
Lỗ đen
Trước khi kết thúc chủ đề này, tôi muốn nói thêm một vài điều liên quan đến lỗ đen. Trái với những gì được phát biểu bởi một trong những diễn giả trong buổi nói chuyện tại VAST mà tôi đề cập bên trên, gần ba mươi năm nay, sự tồn tại của lỗ đen không còn là điều gây tranh cãi; hơn nữa nghiên cứu về lỗ đen là một chủ đề lớn và phong phú của vật lý thiên văn hiện đại. Tất nhiên, những gì ta có thể quan sát được không phải là bản thân lỗ đen vì không có gì, kể cả ánh sáng, có thể thoát ra khỏi lỗ đen nhưng ta nhận được tín hiệu phát ra bởi vật chất chuyển động xoắn ốc xung quanh lỗ đen trước khi bị nuốt chửng. Đặc biệt, lỗ đen Sagittarius A* với khoảng cách gần (chỉ cách chúng ta khoảng 24.000 năm ánh sáng) ở trung tâm thiên hà của chúng ta, Dải Ngân hà, cho phép tiến hành những nghiên cứu rất chi tiết về tính chất của nó. Với một ngôi sao, khi đã đốt cháy phần lớn hydro trở thành heli, các lực điện từ và hạt nhân không còn đủ mạnh, lõi heli suy sụp dưới tác động của trọng lực. Khi ngôi sao ban đầu đủ nặng, lõi của nó có thể đạt đến một kích thước mà vận tốc thoát của một vật từ bên trong lõi đạt đến vận tốc của ánh sáng, không có gì có thể thoát ra được: khi đó một lỗ đen mới được hình thành. Kích thước tới hạn mà điều này xảy ra gọi là bán kính Schwarzschild với giá trị khoảng 5 km trên mỗi khối lượng Mặt trời. Mặt trời của chúng ta không đủ nặng để có thể co lại tới kích thước nhỏ (5 km) như vậy, do đó nó sẽ không trở thành một lỗ đen. Nhưng có nhiều ngôi sao đủ lớn sẽ biến thành lỗ đen, trong đó có nhiều trường hợp đã được nghiên cứu hết sức chi tiết. Lỗ đen như vậy được gọi là những lỗ đen sao, chúng thường di chuyển dần dần về phía tâm thiên hà và cuối cùng bị nuốt bởi hố đen siêu lớn tại đó. Thật vậy, mỗi thiên hà đều có một lỗ đen lớn ở trung tâm của nó, với khối lượng dao động từ một triệu đến một tỷ lần khối lượng mặt trời; Sagittarius A* có khối lượng bằng ba triệu lần khối lượng mặt trời, với khối lượng như vậy đây là một lỗ đen thiên hà tương đối nhỏ. Ngay sau Vụ Nổ lớn (Big Bang), khi các sao và các thiên hà bắt đầu hình thành, Vũ trụ, đã và đang liên tục nở ra, mật độ của Vũ trụ trong quá khứ cao hơn nhiều so với hiện nay. Tương tác giữa các thiên hà xảy ra thường xuyên hơn và sự sáp nhập của các thiên hà là yếu tố quan trọng góp phần vào sự tăng trưởng khối lượng của những lỗ đen thiên hà; vai trò của các lỗ đen ở trung tâm các thiên hà tới sự tiến hóa về khối lượng này chưa được hiểu rõ, đây một chủ đề được tập trung nghiên cứu trong vật lý thiên văn hiện nay.
Điểm cuối cùng liên quan đến mật độ của lỗ đen. Trái ngược với những suy nghĩ phổ biến, giá trị của mật độ không cần phải rất lớn; trong trường hợp lỗ đen sao mật độ rất lớn nhưng với lỗ đen siêu nặng với khối lượng bằng một tỉ lần khối lượng mặt trời có kích thước khoảng 5 109 km và có thể tích 53 1027 kilomet khối, do đó có mật độ 1018 lần nhỏ hơn lỗ đen có khối lượng bằng khối lượng mặt trời. Thật vậy, các lỗ đen siêu nặng có mật độ rất thấp và bản thân Vũ trụ cũng có mật độ rất nhỏ mà ta biết đến, kích thước và khối lượng của Vũ trụ tuân theo mối quan hệ Schwarzscild. Tuy nhiên, Vũ trụ không phải là một lỗ đen vì bên ngoài bán kính Schwarzschild của nó còn nhiều vật chất chứ không phải là chân không như trường hợp của một lỗ đen.Tôi hy vọng rằng những luận điểm sơ sài được phát triển bên trên cho thấy sự phong phú của vật lý liên quan đến câu hỏi tưởng chừng như rất ngây thơ mà từ đó chúng ta đã bắt đầu; như tôi đã nói ở phần đầu, tham vọng duy nhất của tôi là kích thích trí tò mò của người đọc. Dĩ nhiên, có nhiều tài liệu tham khảo thảo luận trực tiếp đến chủ đề này như công trình của Mendel Sach: Thuyết tương đối tổng quát và vật chất, một lý thuyết trường spinor từ kích thước fermi đến năm ánh sáng được Nhà xuất bản Springer phát hành.
Phạm Ngọc Điệp dịch
Tensor ứng suất Cauchy