Mô tả các thí nghiệm vật lý lượng tử: Số phức hay số thực?

Câu trả lời là số phức. Mới đây, hai nhóm nghiên cứu độc lập đã cho thấy cơ học lượng tử phải cần đến số phức chứ không phải số thực để tái tạo các kết quả thực nghiệm.

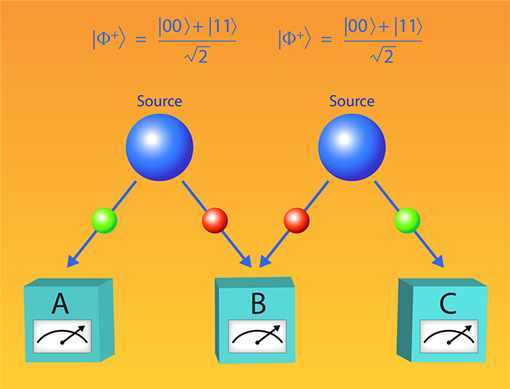
Hình 1: Phác thảo trò chơi lương tử ba bên được sử dụng bởi nhóm của Chen và nhóm của Li nhằm chứng minh rằng lý thuyết lượng tử dựa trên số thực không thể mô tả đưoc kết quả thông kê của một số phép đo trên các mạng lượng tử nhỏ. Trong trò chơi có hai nguồn phân phối các qubit rối cho ba người chơi là những người sẽ tính toán “điểm số” đạt được từ các kết quả của các phép đo trên các qubit mà họ nhận được từ các nguồn phân phối qubit rối. 

Số phức được sử dụng rộng rãi trong vật lý cổ điển và vật lý tương đối tính. Ví dụ, trong điện từ học, sử dụng số phức đơn giản hóa rất nhiều việc mô tả các hiện tượng dạng sóng. Tuy nhiên, đối với các hiện tượng này số phức không hoàn toàn cần thiết, vì tất cả các số liệu quan sát được đều có thể biểu thị được bằng việc sử dụng số thực. Vì vậy, sử dụng số phức chỉ được coi như một công cụ tính toán thuận tiện. Nhưng vai trò của số phức là gì trong vật lý lượng tử khi các khái niệm cơ bản của nó (như hàm sóng, không gian Hilbert, v.v.) về bản chất là phức? Câu hỏi đơn giản này đã đồng hành cùng sự phát triển của cơ học lượng tử kể từ khi nó ra đời: chính những người sáng lập ra nó như Schrödinger, Lorentz, Planck … đã tranh luận về vấn đề này (xem các thư của họ 1).

Từ rất sớm, những người tiên phong của cơ học lượng tử đã không phát triển lý thuyết lượng tử dựa trên các số thực vì họ cho rằng nó không thuận tiện trong tính toán lý thuyết. Tuy nhiên, sử dụng các số thực chưa bao giờ bị loại trừ một cách chính thức. Các kết quả lý thuyết gần đây cho thấy lý thuyết lượng tử dựa trên các số thực có thể mô tả rất nhiều hệ lượng tử khác nhau 2. Nhưng mới đây lý thuyết lượng tử dựa trên số thực đã bị bác bỏ bằng thực nghiệm của hai nhóm nghiên cứu độc lập, một nhóm do Ming-Cheng Chen ở Đại học Khoa học và Công nghệ Trung Quốc chủ trì 3 và một nhóm do Zheng-Da Li của Đại học Khoa học và Công nghệ Nam Trung Quốc chủ trì 4. Cả hai nhóm đều chỉ ra, buộc phải sử dụng số phức trong cơ học lượng tử để mô tả kết quả của các thí nghiệm trên mạng lượng tử đơn giản.

Điểm xuất phát cơ bản của lý thuyết lượng tử là biểu diễn trạng thái của một hạt bằng một véc tơ trong không gian phức, gọi là không gian Hilbert. Tuy nhiên, việc mô tả một hệ lượng tử riêng lẻ dựa hoàn toàn vào các số thực cũng rất đơn giản: chỉ cần nhân đôi số chiều của không gian Hilbert, vì không gian phức là tương đương, hoặc “đẳng cấu”, với mặt phẳng thực hai chiều (một chiều biểu diễn phần thực và chiều kia là phần ảo của số phức). Vấn đề trở nên ít hiển nhiên hơn khi xét tới các tương quan lượng tử kỳ lạ trong cơ học lượng tử như rối lượng tử chẳng hạn. Rối lượng tử có thể phá vỡ nguyên tắc hiện thực cục bộ (local realism), như đã được chứng minh và kiểm chứng thông qua cái gọi là bất đẳng thức Bell 5. Thoạt đầu số phức được cho là thiết yếu để có thể mô tả sự vi phạm bất đẳng thức Bell 6. Nhưng vào năm 2009, một công trình lý thuyết đã chứng minh rằng sử dụng số thực vẵn có thể tái tạo kết quả thống kê của bất kỳ thí nghiệm Bell chuẩn nào, kẻ cả những thí nghiệm trên nhiều hệ lượng tử 2. Kết quả này củng cố giả thuyết số phức là không cần thiết. Nhưng việc vẫn chưa có bằng chứng tổng quát về sự tương đương giữa lý thuyết lượng tử “phức” (dựa trên số phức) và lý thuyết lượng tử “thực” (dựa trên số thực) đã mở đường cho những nghiên cứu sâu sắc hơn về vấn đề này.  

Số phức vượt số thực

Mới đây, một nghiên cứu như vậy đã xuất hiện vào năm 2021. Đó là một công trình lý thuyết xuất sắc của Marc-Olivier Renou thuộc Viện Khoa học Quang tử ở Tây Ban Nha và các đồng nghiệp 7. Các tác giả đã xét đồng thời cả hai lý thuyết (“phức” và “thực”): một lý thuyết dựa trên các tiên đề chuẩn của cơ học lượng tử (tức là sử dụng không gian Hilbert phức như trong cách tiếp cận truyền thống), còn lý thuyết kia sử dụng không gian thực. Sau đó, họ nghĩ ra cách thiết kế các thí nghiệm kiểu như thí nghiệm Bell nhưng có sự mở rộng thích hợp nhằm chứng minh sự không phù hợp của lý thuyết lượng tử dựa trên các số thực.  Các thí nghiệm đó về lý thuyết có thể mô tả như sau. Hai nguồn độc lập tạo ra và phân phối các cặp qubit rối tới các nút khác nhau trong một mạng lượng tử. Tại mỗi nút các phép đo độc lập được tiến hành và các kết quả đo tiết lộ các mối tương quan lượng tử mà không có lý thuyết lượng tử “thực” (dựa trên số thực) nào có thể thiết lập được.

Nhóm của Chen và nhóm của Li đồng thời tiến hành thử nghiệm theo đề xuất của Renou và đồng nghiệp nhưng ở hai nền tảng vật lý khác nhau. Các thử nghiệm được diễn đạt như một “trò chơi” trong đó ba người chơi, Alice, Bob và Charlie, thực hiện các thao tác kiểu Bell mở rộng như trên Hình 1. Có hai nguồn tạo các cặp qubit rối. Một nguồn phân phối các qubit rối cho Alice và Bob, nguồn còn lại phân phối các qubit rối cho Bob và Charlie. Mỗi người chơi lựa chọn một cách độc lập các phép đo từ một tập hợp xác định để đo các qubit của mình. Vì hai nguồn rối là độc lập với nhau, các qubit mà Alice và Charlie nhận được hoàn toàn không có tương quan nào với nhau. Bob nhận được hai qubit từ cả hai nguồn và thực hiện phép đo Bell trên hai qubit đó. Bằng cách ấy Bob tạo ra rối giữa các qubit của Alice và Charlie, mặc dù các qubit của Alice và Charlie không hề tương tác với nhau (theo hiện tượng “tráo rối” (“entanglement swapping”) trong cơ học lượng tử [8]). Sau đó, một “điểm số” được tính toán theo phân phối thống kê của các kết quả đo. Đúng như đã được chứng minh bằng lý thuyết bởi Renou và các đồng nghiệp, lý thuyết lượng tử phức (dựa trên các số phức) có thể đạt được một điểm số lớn hơn điểm số mà lý thuyết lượng tử thực có thể.

Hai nhóm nghiên cứu đã có các cách tiếp cận khác nhau đối với trò chơi lượng tử nói trên. Nhóm của Chen sử dụng một bộ xử lý lượng tử siêu dẫn, trong đó các qubit có thể điều khiển được và đo được một cách riêng lẻ. Thách thức chính và rất nghiêm ngặt của cách tiếp cận này là phải làm cho các qubit trên cùng một mạch siêu dẫn thực sự độc lập và tách rời với nhau. Nhóm của Li lại chọn cách tiếp cận quang tử để dễ đạt được sự độc lập và tách rời giữa các qubit hơn. Cụ thể, họ sử dụng các photon rối phân cực được tạo ra bởi quá trình chuyển đổi tham số và được đếm trong các máy dò đơn photon dây nano siêu dẫn. Tuy nhiên, cách tiếp cận quang tử lại chịu một thách thức khác: Giao thức do Renou và các đồng nghiệp đề xuất yêu cầu các phép đo trạng thái Bell phải là hoàn hảo (từng trạng thái Bell phải được phân biệt chính xác 100%). Phép đo Bell hoàn hảo có thể thực hiện được trên các qubit siêu dẫn nhưng lại  không thể trên các quang tử với các thiết bị quang học tuyến tính. Do đó, Li và các đồng nghiệp phải dựa vào phép đo Bell không hoàn hảo (tức là từng trạng thái Bell không phân biệt chính xác được).

Bất chấp những khó khăn vốn có trong mỗi cách tiếp cận, kết quả của cả hai thử nghiệm của nhóm Cheng và nhóm Li đều rất thuyết phục. Điểm số của lý thuyết phức đã vượt trội điểm số của của lý thuyết thực (độ lệch chuẩn giữa lý thuyết phức và lý thuyết thức lần lượt là 43 sigma và 4.5 sigma trong cách tiếp cận của nhóm Chen và nhóm Li). Đó là bằng chứng thuyết phục sự cần thiết của số phức trong mô tả các thí nghiệm vật lý lượng tử.

Khối cơ bản của internet lượng tử

Điều thú vị là thí nghiệm của cả hai nhóm đều dựa trên một sơ đồ mạng lượng tử tối thiểu, chỉ gồm hai nguồn tạo rối và ba nút đo. Đó là một khối nền tảng cơ bản đầy hứa hẹn cho việc tạo dựng các mạng internet lượng tử trong tương lai. Vì vậy, các kết quả thu được cung cấp thêm một minh chứng về việc các công nghệ lượng tử mới hiện có có mối liên hệ chặt chẽ với khả năng có thể kiểm tra các khía cạnh cơ bản của cơ học lượng tử. Ngược lại, những hiểu biết cơ bản mới này về cơ học lượng tử có thể có những tác động bất ngờ đối với sự phát triển của các công nghệ thông tin lượng tử mới.

Một điều đáng lưu ý là chúng ta phải thận trọng khi đánh giá tác động của những kết quả này. Người ta có thể dễ bị cám dỗ và đi đến kết luận rằng số phức là không thể thiếu để mô tả thực tại vật lý của Vũ trụ. Tuy nhiên, kết luận như vậy chỉ đúng nếu chúng ta chấp nhận khung chuẩn của cơ học lượng tử dựa trên một số tiên đề cụ thể. Như Renou và các đồng nghiệp đã chỉ ra, những kết quả này sẽ không thể áp dụng cho các khung thay thế khác của cơ học lượng tử, chẳng hạn như khung của cơ học Bohmian, là khung dựa trên các tiên đề khác so với khung chuẩn thông thường. Cơ học lượng tử xây dựng trong khuôn khổ của khung chuẩn với những thành công to lớn trong việc giả thích/tiên đoán các kết quả thực nghiệm là không thể phủ nhận, nhưng theo quan điểm diễn giải (interpretative point of view) nó vẫn bị coi là không đầy đủ [9]. Do đó, những kết quả được nói tới ở đây có thể kích thích những nỗ lực vượt ra ngoài khung chuẩn của cơ học lượng tử.

Nguyễn Bá Ân dịch

Nguồn: http://vnlib.kias.re.kr/87656e7/_Lib_Proxy_Url_Https/physics.aps.org/articles/v15/7

——————————–

Tài liệu tham khảo 
1. C. N. Yang, “Square root of minus one, complex phases and Erwin Schrödinger,” Selected Papers II with Commentary (World Scientific, Hackensack, 2013) 
2. M. McKague et al., “Simulating quantum systems using real Hilbert spaces,” Phys. Rev. Lett. 102, 020505 (2009).
3. M.-C. Chen et al., “Ruling out real-valued standard formalism of quantum theory,” Phys. Rev. Lett. 128, 040403 (2022).
4. Z.-D. Li et al., “Testing real quantum theory in an optical quantum network,” Phys. Rev. Lett. 128, 040402 (2022).
5. A. Aspect, “Closing the door on Einstein and Bohr’s quantum debate,” Physics 8, 123 (2015).
6. N. Gisin, “Bell Inequalities: Many Questions, a Few Answers,” in Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle, edited by W. C. Myrvold et al. The Western Ontario Series in Philosophy of Science, Vol. 73 (Springer, Dordrecht, 2009).
7. M.-O. Renou et al., “Quantum theory based on real numbers can be experimentally falsified,” Nature 600, 625 (2021).
8. J.-W. Pan et al., “Experimental entanglement swapping: Entangling photons that never interacted,” Phys. Rev. Lett. 80, 3891 (1998).
9. T. Norsen, Foundations of Quantum Mechanics – An Exploration of the Physical Meaning of Quantum Theory, Undergraduate Lecture Notes in Physics (Springer, Cham, 2017).

Tác giả

(Visited 26 times, 1 visits today)