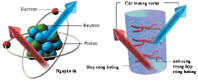
Một vấn đề thời sự : Nguyên lý tương đối, nguyên lý cơ sở của các lý thuyết Einstein có bị vi phạm ?

Nguyên lý tương đối nằm ở tâm của tất cả lý thuyết cơ bản của vật lý. Vậy nguyên lý đó là gì?
Nguyên lý tương đối được Einstein phát biểu khi xây dựng lý thuyết tương đối hẹp vào năm 1905: mọi định luật vật lý là như nhau trong các hệ quán tính (tức các hệ chuyển động thẳng đều theo một hướng bất kỳ). Những hệ quả quan trọng của nguyên lý tương đối: tốc độ ánh sáng c là một hằng số, đồng hồ đang chuyển động chạy chậm hơn, độ dài của vật đang chuyển động bị co lại và năng lượng với khối lượng được liên hệ với nhau bởi công thức nổi tiếng của Einstein E = mc2. Những hệ quả đó đã trở thành cơ sở của mọi thí nghiệm, ứng dụng thường nhật. Ví như trong hệ định vị toàn cầu (GPS-Global Positioning System) người ta cũng phải tính đến hệ quả giãn nở thời gian để chỉnh lý các đồng hồ trên vệ tinh quỹ đạo. Nói cách khác hiện nay nguyên lý tương đối gần như là một chân lý tuyệt đối.
Nhưng trong quá trình xây dựng một lý thuyết thống nhất nhiều nhà vật lý đã nghiên cứu khả năng vi phạm nguyên lý tương đối và cho rằng nguyên lý thiêng liêng này chỉ là một nguyên lý gần đúng của thiên nhiên [1, 2, 3, 4]. Họ hy vọng rằng những vi phạm nguyên lý tương đối chính là nguyên nhân gây khó khăn trong việc thống nhất hai lý thuyết lượng tử và hấp dẫn. Cho nên việc đưa vào lý thuyết các yếu tố vi phạm nguyên lý tương đối có thể mở đường cho một lý thuyết thống nhất được mong đợi từ lâu.

Sự vi phạm đối xứng Lorentz có thể gây nên bởi một trường vectơ (biểu diễn bằng mũi tên đỏ). Hạt và lực có tương tác với trường vectơ đó . Hệ quả là: các hướng và các vận tốc bây giờ không còn là tương đương với nhau nữa. Hai thanh vật chất khác nhau song có cùng một độ dài theo một hướng nào đó sẽ có thể co lại hay giãn ra theo một hướng khác. Tương tự như thế hai đồng hồ khác nhau nếu chạy đồng bộ lúc ban đầu trong một hướng nào đó có thể chạy chậm hoặc chạy nhanh hơn trong một hướng khác ban đầu. Ngoài ra hai thanh vật chất và hai đồng hồ khác nhau có thể bị co giãn và chạy chậm nhanh tùy theo vật liệu làm nên chúng và khi nâng vận tốc của chúng lên (xem các mũi tên đen bên cực phải của hình vẽ 2).

Tính bất biến của các định luật đối với các hệ quán tính là biểu hiện của một đối xứng không thời gian có tên là đối xứng Lorentz (do nhà vật lý thuyết người Đức Hendrik Antoon Lorentz đề ra năm 1890). Theo đối xứng này những định luật vật lý sẽ như nhau trong mọi hệ quán tính bất kể chiều hướng và vận tốc của nó. Khi có bất biến Lorentz thì không thời gian là đẳng hướng theo mọi hướng và mọi chuyển động thẳng đều là tương đương với nhau.
Khi kết hợp với thuyết lượng tử, đối xứng Lorentz chúng ta có lý thuyết trường lượng tử tương đối. Mô hình chuẩn SM (Standard Model) mô tả mọi hạt cơ bản và các tương tác giữa chúng với nhau (điện từ, yếu, mạnh – song chưa có hấp dẫn) là một lý thuyết trường tương đối. Mọi tương tác khả dĩ song không bất biến Lorentz đều bị loại khỏi SM.
Lý thuyết hấp dẫn của Einstein cũng tuân theo một cách định xứ (local) đối xứng Lorentz, nếu xét toàn cục (global) thì có nguyên lý tương đương. Hiện nay người ta tìm cách thống nhất mô hình chuẩn SM với lý thuyết hấp dẫn GR. Hai lý thuyết SM và GR đều có những cấu trúc tuyệt đẹp riêng song chưa tương thích về mặt toán học để có thể được thống nhất.

Nếu thống nhất thì SM và GR phải hòa hợp với nhau ở những vùng có kích thước Planck (cỡ 10-35 m). Hiện nay khả năng kiểm nghiệm của chúng ta giới hạn ở vùng kích thước 10-19 m. Tuy nhiên chúng ta có cách tiếp cận vấn đề này. Tình huống tương tự như khi nhìn vào màn hình tivi, mọi hình ảnh được tạo bởi rất nhiều pixel không phân biệt được song nếu nhìn vào một chiếc càvát có nhiều đường kẻ nhỏ trên ngực một phát thanh viên thì những đường kẻ này tạo nên một ảnh Moiré và ảnh Moiré này là biểu hiện tương tự của khả năng thấy được những vi phạm nguyên lý tương đối. Trên một khoảng cách vĩ mô thì nguyên lý tương đối bảo toàn song ở những khoảng cách Planck thì đối xứng này có thể  bị vi phạm.
Một đối xứng cơ bản khác của không thời gian là đối xứng CPT [8]. SM thỏa mãn bất biến CPT song các lý thuyết với vi phạm nguyên lý tương đối có thể phá vỡ đối xứng CPT.

Phá vỡ đối xứng tự phát
Nếu tồn tại một trường phông vectơ (hay tenxơ nói chung) thì vectơ này ấn định một hướng do đó phá vỡ đối xứng (Phá vỡ đối xứng tự phát). Nếu hiện tượng phá vỡ đối xứng tự phát nằm trong cơ chế của lý thuyết thì sự phá vỡ nguyên lý tương đối sẽ xuất hiện kèm theo.
Khi bất biến Lorentz bị phá vỡ đối xứng tự phát thì những trường phông tàn dư – chính là các trường vectơ hoặc tenxơ nói trên– sẽ chiếm đầy không gian và xác định một hướng tự phát ưu tiên nào đó.
Một hạt cơ bản chuyển động trong các trường phông đó sẽ tương tác với chúng. Sự có mặt của trường phông sẽ phá vỡ đối xứng Lorentz dẫn đến những thay đổi trong chuyển động hoặc hướng của spin của hạt so với các trường tàn dư đó.

Mô hình chuẩn mở rộng SME (Standard Model Extension)
Giả sử rằng lý thuyết có chứa vi phạm đối xứng Lorentz. Thử hỏi điều này sẽ biểu hiện trong các thí nghiệm như thế nào? Và gắn liền với những lý thuyết đã biết theo cách nào?
Để trả lời các câu hỏi này chúng ta cần có một lý thuyết mô tả bao trùm các hệ quả thực nghiệm đó. Một lý thuyết như thế phải chứa những yếu tố vi phạm đối xứng Lorentz nhỏ (vì đối xứng Lorentz được bảo toàn về tổng thể). Như thế khi thống nhất SM và GR ta phải đưa vào lý thuyết những hạng số nhỏ mô tả tất cả các tương tác khả dĩ ( possible interactions). Mỗi số hạng sẽ ứng với một trường vectơ hoặc tenxơ đặc biệt với giá trị phông khác số không. Một lý thuyết như thế là SME.
Hàm tác động trong SME có dạng
                                              S SME = S SM + S LV + S GR
Trong đó S LV chứa những số hạng gây vi phạm đối xứng Lorentz (LV- Lorentz violations) với những hệ số mà chúng ta phải xác định từ thực nghiệm. Các số hạng này mô tả tương tác các trường vectơ (hoặc tenxơ) này với các trường vật chất của các loại hạt và hấp dẫn. Những hệ số phải xác định đóng vai trò các trường vectơ và tenxơ tàn dư nói trên.
Để biểu kiến các hệ quả của vi phạm đối xứng Lorentz, cần cho rằng không thời gian có một hướng nội tại nào đó (vậy phá vỡ đối xứng). Trong trường hợp tồn tại một trường vectơ ứng với một số hạng trong các phương trình của SME thì hướng nội tại nói trên trùng với hướng của trường vectơ. Trong trường hợp tổng quát hơn ta sẽ có những trường tenxơ. Vì có tương tác với các trường đó mà sự tương tác cũng như chuyển động của các hạt sẽ phụ thuộc vào hướng nói trên, giống như sự chuyển động của các hạt mang điện tích trong điện trường hay từ trường.
Một tình huống như thế cũng xảy ra đối với vi phạm CPT [5] song ở đây hệ quả vi phạm xảy ra vì hạt và phản hạt có hằng số tương tác khác nhau đối với các trường phông.
Oscar Greenberg (Đại học Maryland) chứng minh rằng nếu CPT bị vi phạm thì bất biến Lorentz sẽ bị phá vỡ. Điều đó có nghĩa là mọi lý thuyết chứa vi phạm CPT và tương thích với SM sẽ thuộc về SME.
Cần nói thêm rằng tính chất và tương tác của các hạt phụ thuộc vào hướng chuyển động (vi phạm đối xứng quay) và cả vào vận tốc của chúng (boost violations – chữ boost ở đây có nghĩa là nâng vận tốc lên). Các hệ quả vi phạm còn phụ thuộc vào spin, vào màu sắc của hạt (hệ quả đối với proton sẽ khác đối với neutron).
Sự vi phạm nguyên lý tương đối sẽ gây nên sự khác nhau trong hiện tượng phân cực đối với ánh sáng  vùng hồng ngoại, vùng thấy được và vùng cực tím khi ánh sáng đi từ những thiên hà nằm xa chúng ta (thí nghiệm đang được tiến hành tại Đại học Indiana).
 

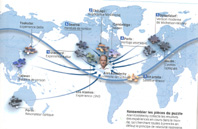Các địa điểm trên thế giới đang tiến hành thí nghiệm nhằm tìm những vi phạm nguyên lý tương đối.

Một số thí nghiệm đang được tiến hành trên thế giới nhằm phát hiện các vi phạm nguyên lý tương đối
1/Năm 2003 John Lipa và cộng sự tại Đại học Stanford lặp lại thí nghiệm Michelson-Morley trong một phương án hiện đại hơn, có độ nhạy cao hơn. Họ so sánh tần số cộng hưởng của hai hộp cộng hưởng quang học đặt thẳng góc nhau trong một thời gian nhiều tháng. Dấu hiệu vi phạm bất biến Lorentz là sự khác nhau giữa hai tần số cộng hưởng khi quả đất quay.
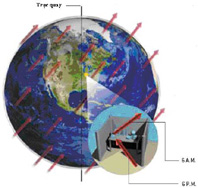
2/So sánh biến đổi khối lượng của hai vật theo các hướng khác nhau so với hướng phá vỡ đối xứng (xem hình 4).

Hình 4

Chuyển động quay của quả đất sẽ làm quay một phòng thí nghiệm, như phòng thí nghiệm tại Đại học Indiana (điểm màu vàng trên hình vẽ 4) đối với một trường vectơ (biểu diễn bởi các mũi tên). Trường vectơ thay đổi hướng trong vòng một ngày cho phép ghi nhận các vi phạm bất biến Lorentz. Ví dụ quá trình so sánh 2 khối lượng khác nhau trong phòng thí nghiệm có thể cho chúng ta thấy những thay đổi nhỏ có chu kỳ của chúng.

3/So sánh hai đồng hồ (xem các hình 5A, 5B, 5C)
Trên một trạm vũ trụ (hình vẽ 5 A) chúng ta có thể tiến hành thí nghiệm tìm các vi phạm bất biến Lorentz bằng cách so sánh các đồng hồ. Hình vẽ minh họa trường hợp có hai trường vectơ (hình vẽ 5A, 5B) gây nên vi phạm nguyên lý tương đối (mô tả bởi các mũi tên đỏ và xanh) với những tương tác khác nhau đối với các hạt. Ta có một đồng hồ nguyên tử (hình vẽ 5B) và một đồng hồ dựa trên vi sóng ánh sáng (hình vẽ 5C– các đường sóng). Các electron (màu đỏ) tương tác với trường vectơ màu đỏ. Các proton (màu xanh) tương tác với trường vectơ xanh. Khi trạm vũ trụ quay thì các đồng hồ sẽ chạy đồng bộ hoặc không đồng bộ, biểu hiện các vi phạm bất biến Lorentz.
 

                                                                   
4/So sánh phổ của vật chất và phản vật chất
Thí nghiệm về vật chất (bên trái hình vẽ 6) và phản vật chất (bên phải hình vẽ 6). Vật chất và phản vật chất sẽ có hành vi như nhau nếu có bất biến CPT [5] như vậy phổ của chúng (bên dưới hình vẽ 6) sẽ như nhau. Và mọi sự khác biệt trong phổ của chúng sẽ nói lên có vi phạm CPT, và từ đó là vi phạm bất biến Lorentz.

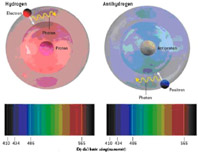Hình 6

 5/Sự phụ thuộc vi phạm bất biến Lorentz vào spin (xem hình 7)
Tại Đại học Washington người ta đã tiến hành thí nghiệm sau đây để tìm hiểu vi phạm bất biến Lorentz gây nên bởi các spin. Trên hình là một đồng hồ xoắn, vai trò quả lắc thông thường (lắc qua lại) ở đây được đảm nhiệm bởi một quả xoắn (xoắn trái rồi xoắn phải). Quả xoắn được làm bằng những thanh nam châm (đỏ và xanh, xem bên phải hình vẽ 7) và được cấu tạo sao cho tổng spin các electron khác số không. Đồng hồ được đặt trên một mâm quay. Nếu có vi phạm đối xứng Lorentz thì người ta sẽ ghi đo được các nhiễu loạn của dao động.

Hình 7.

 Kết luận
Thibault Damour, IHES (Institut des Hautes Etudes Scientifiques) cho rằng lý thuyết dây (String theory) có cấu trúc cho phép xét đến những vi phạm bất biến Lorentz [6]. Tương tự như vậy Carlo Rovelli (Centre de physique théorique, Université de Marseille) cũng khẳng định rằng lý thuyết lượng tử vòng (Loop quantum theory) [7] không loại khả năng đưa vào những vi phạm nguyên lý tương đối. Song hai nhà lý thuyết này đều cho rằng chưa có cơ sở chắc chắn để đưa vi phạm đối xứng Lorentz vào các lý thuyết vừa nêu.
Một lý thuyết quan trọng khác là Hình học không giao hoán của Alain Connes cũng chứa tiềm năng cho phép đề cập đến vi phạm bất biến Lorentz [8].
Hiện nay mặc dù nhiều cố gắng của các nhà thực nghiệm, các kết quả thực nghiệm ban đầu cho những vi phạm quá ư là nhỏ và nằm trong phạm vi sai số do đó khó có thể kết luận một cách chắc chắn có vi phạm bất biến Lorentz, song nhiều nhà vật lý vẫn tin rằng manh nha có những dấu hiệu đầu tiên của vi phạm nguyên lý tương đối và do đó tiếp tục tiến hành các thí nghiệm.
Như vậy Einstein vẫn đúng đến thời điểm hiện nay (Graham P. Collins, [4]), song trong tương lai người ta chưa biết liệu các lý thuyết Einstein có phải chỉ là một lý thuyết gần đúng mà thôi hay không?

Tài liệu tham khảo:
[1] Q G Bailey Q G, Alan Kostelecky,   Phys. Rev. D 74 045001/ 2006
[2] Alan Kostelecky, Physical Review D, tháng 12 năm 2003
[3] Cécile Bonneau, Science & Vie, tháng 7 năm 2006
[4] Alan Kostelecky, Scientific American, tháng 7 năm 2004
[5] CPT là tích của 3 phép biến đổi: C – thay hạt bằng phản hạt và ngược lại, P – phép nghịch đảo không gian và T – phép nghịch đảo thời gian.
[6] Cao Chi, Einstein và vũ trụ lượng tử, Einstein với khoa học & công nghệ hiện đại. Hội vật lý thành phố Hồ Chí Minh, 2005. Lý thuyết dây cho rằng các hạt và hấp dẫn phát sinh từ dao động của dây và màng
[7] Lee Smolin, Atoms of space & time, Scientific American, tháng 1 năm 2004. Lý thuyết vòng lượng tử  cho rằng không thời gian không  liên tục và phải được lượng tử hóa.    
[8] Cao Chi, Hình học không giao hoán: Một quan điểm cách mạng về không thời gian. Tia Sáng số 19- 05/10/2006. Hình học không giao hoán cho rằng các tọa độ không- thời gian không giao hoán với nhau.