Tác động của khoa học và công nghệ đến phát triển kinh tế: Cần cẩn thận trong cách diễn giải kết quả
Trong một phân tích về mối liên hệ giữa phát triển kinh tế và năng lực công nghệ gần đây [1], hai tác giả kết luận rằng “khi chỉ số năng lực công nghệ chung tăng 1% thì chỉ số phát triển kinh tế sẽ tăng thêm được 1,2298%; sự phát triển kinh tế của Việt Nam giai đoạn 2001-2005 có liên quan đến yếu tố năng lực công nghệ là 73,52%.” Tuy nhiên, đọc kĩ bản phân tích, tôi nghĩ cách diễn giải trên có lẽ không phù hợp với số liệu, và quan trọng hơn có vài vấn đề về phương pháp phân tích có thể ảnh hưởng đến sự hợp lí của kết luận này. Bài viết ngắn này sẽ bàn qua ba vấn đề chính: diễn giải kết quả phân tích, mô hình phân tích, và vấn đề logic trong suy luận quần thể.
Tóm lược kết quả phân tích
Để đánh giá mức độ tác động của khoa học và công nghệ đến phát triển kinh tế, các tác giả đã tiến hành một công trình nghiên cứu có thể nói là “tham vọng”, bằng cách điều tra và thu thập dữ liệu từ 34 tỉnh / thành (tôi sẽ gọi tắt là “địa phương” cho tiện) trên bình diện toàn quốc. Các dữ liệu chính liên quan đến bài viết gồm 4 chỉ số sau đây:
* chỉ số đổi mới công nghệ (doimoi);
* chỉ số chuyển giao công nghệ (chuyengiao); và
* chỉ số công nghệ thông tin và truyền thông (cntt).
Ngoài 3 chỉ số doimoi, chuyengiao, và cntt, một chỉ số khác có tên là “năng lực công nghệ” (nangluc) được tính toán theo công thức sau:
Hai tác giả tiến hành phân tích mối liên hệ giữa kinhte và nangluc qua mô hình hồi qui tuyến tính như sau:
kinhte = a + b×nangluc + e [1]
Mô hình có hai thông số: a phản ảnh chỉ số kinh tế trung bình khi nangluc=0 (còn gọi là intercept), và b là hệ số liên quan đến chỉ số năng lực (còn gọi là gradient). Do đó, a+b×nangluc chính là giá trị kì vọng hay chỉ số phát triển kinh tế trung bình với một chỉ số năng lực công nghệ trung bình. Mô hình còn có e là phần dư (residuals), tức là phần không thể giải thích bằng a + b×nangluc. Qua phân tích số liệu thực tế, các tác giả có được phương trình như sau:
kinhte = -0,1023 + 1,1298×nangluc
và diễn giải rằng “khi chỉ số năng lực công nghệ tăng lên 1% thì chỉ số phát triển kinh tế sẽ tăng thêm được 1,2298%”, và “với hệ số xác định R2 = 0,7352. Nghĩa là, trong điều kiện cụ thể của Việt Nam, sự tăng lên của phát triển kinh tế trong giai đoạn 2001-2005 được giải thích liên quan đến yếu tố năng lực công nghệ là 73,52%.” Xin mở ngoặc ở đây để nói thêm rằng có lẽ các tác giả viết nhầm 1,1298 thành 1,2298.
Tuy nhiên, tôi e rằng cách diễn giải này không phù hợp với số liệu thực tế (vì thông số liên quan đến nangluc là 1,1298) và quan trọng hơn là phương pháp phân tích có thể có vấn đề về logic. Do đó, ở đây, tôi chỉ bàn đến ba vấn đề chính: diễn giải, mô hình phân tích, và logic.
Trước hết, khi phân tích bằng mô hình hồi qui tuyến tính giữa giữa kinhte và nangluc, tôi không có cùng kết quả với các tác giả. Thật ra, ngay cả các phương trình trong bài báo tôi đều có kết quả khác với hai tác giả, nhưng đây là một lĩnh vực khác và tôi không muốn bàn sâu trong bài viết này [2]. Các thông số mà tôi có được là (bạn đọc có thể kiểm tra bằng máy tính dễ dàng):
kinhte = -10,23 + 1,13×nangluc
Rất có thể các tác giả đã lấy thông số đầu chia cho 100 để có được hằng số -0,1023. Nhưng chúng ta không rõ tại sao lại chia hằng số (intercept) này cho 100, và cách tính như thế có ý nghĩa gì.
Để thấy cách diễn giải của các tác giả không đúng với thực tế, chúng ta có thể lấy hai địa phương với nangluc là 40 và 41, và theo phương trình trên, chỉ số kinhte dự đoán là:
kinhte = -10,23 + 1,13×40 = 34,97
và
kinhte = -10,23 + 1,13×41 = 36,10
như vậy, địa phương có chỉ số năng lực cao hơn 1 đơn vị có chỉ số (dự đoán) phát triển kinh tế cao hơn 3,2% (lấy 36,10 chia cho 34,97 và nhân cho 100).
Nhưng nếu hai địa phương khác có chỉ số nangluc là 60 và 61, thì chỉ số kinhte dự đoán lần lược là 57,57 và 58,70, tức độ khác biệt khoảng 1,9%.
Qua cách tính đơn giản trên, chúng ta thấy không thể nào diễn giải như tác giả được, bởi vì: (a) đơn vị của chỉ số phát triển kinh tế không phải là số phần trăm, (b) đơn vị của chỉ số năng lực công nghệ cũng không phải là số phần trăm, và (c) không có thông số nào liên quan đến thời gian trong mô hình để phát biểu rằng “sẽ tăng thêm được 1,2298%”. Xin nhấn mạnh rằng các số liệu này được thu thập trong quá khứ (2001 – 2005) và thông số được ước tính từ số liệu trong quá khứ, nên không thể diễn giải về tương lai (“sẽ”) được.
Thật ra, mô hình kinhte = -10,23 + 1,13×nangluc phải được hiểu như sau: nếu chỉ số bình quân về năng lực công nghệ giữa bất cứ hai địa phương nào khác nhau 1 đơn vị thì chỉ số bình quân về phát triển kinh tế giữa hai địa phương khác nhau 1,13 đơn vị. Cụm từ “khác nhau” ở đây có nghĩa là cao hay thấp, chứ không hẳn có nghĩa là “tăng”, bởi vì không có yếu tố thời gian trong phương trình trên, mà chỉ có khác biệt giữa các địa phương. Ngoài ra, chúng ta chưa biết chính xác đơn vị đo lường của hai chỉ số kinhte và nangluc là gì, nên chỉ có thể diễn giải chung là “đơn vị”, chứ không thể phần trăm.
Để biết được mức độ hữu dụng của phương trình (hay mô hình) chúng ta có thể so sánh phương sai (variance) trước và sau khi mô hình hóa. Phương sai gốc của chỉ số kinhte là 180,37. Sau khi điều chỉnh cho ảnh hưởng của chỉ số nangluc qua mô hình [1], phương sai của kinhte là 49,26, tức giảm khoảng 73% so với phương sai trước khi mô hình hóa. Nói cách khác, cách diễn giải hệ số này là: những khác biệt về chỉ số năng lực kinh tế giữa các địa phương có thể giải thích khoảng 73% độ dao động (variation) của chỉ số phát triển kinh tế (chứ không phải “sự tăng lên của phát triển kinh tế”) giữa các địa phương.
Hệ số 73% là một ảnh hưởng rất lớn. Và, điều này làm cho chúng ta phải suy nghĩ: có phải năng lực công nghệ giải thích đến 73% những khác biệt về phát triển kinh tế giữa các địa phương, hay đây chỉ là một sai lầm trong mô hình phân tích?
Vấn đề mô hình dựa vào số trung bình
Như đề cập trên, các tác giả tiến hành phân tích dữ liệu bằng hai bước: bước 1 là tính toán bình quân cho mỗi chỉ số trong thời gian 2001 đến 2005, và bước hai là ứng dụng mô hình hồi qui tuyến tính cho các chỉ số bình quân. Cách phân tích này nảy sinh một vấn đề nghiêm trọng: đó là vấn đề dựa vào số trung bình.
Phân tích dựa vào chỉ số bình quân rất dễ dẫn đến kết luận sai lầm và lạc quan. Có khi trong thực tế không có mối liên hệ nào giữa hai chỉ số ở mỗi địa phương, nhưng khi phân tích dựa vào số trung bình cho các địa phương thì lại có mối liên hệ! Nói cách khác, phân tích dựa vào chỉ số trung bình có thể dẫn đến kết luận sai lầm và thiếu khách quan như giải thích trong phần chú thích 3 dưới đây [3].
Để hiểu thêm vấn đề, chúng ta cần lưu ý đơn vị phân tích và câu hỏi nghiên cứu ở đây. Theo tôi, câu hỏi nghiên cứu thật sự là: ở một địa phương, nếu chỉ số năng lực công nghệ gia tăng giữa các năm 2001, 2002, 2003, 2004, và 2005 có tác động đến chỉ số phát triển kinh tế hay không.
Qua câu hỏi trên, chúng ta thấy đơn vị phân tích là chỉ số qua 5 năm cho từng địa phương. Nói cách khác, chỉ khi nào mối liên hệ giữa năng lực công nghệ và phát triển kinh tế được quan sát ở tất cả (hay phần lớn) địa phương thì chúng ta mới có thể nói rằng khi chỉ số năng lực công nghệ tăng thì chỉ số phát triển kinh tế cũng tăng theo. Vì phân tích theo thời gian, chúng ta có thể sử dụng động từ “tăng” ở đây. (Ở đây xin mở ngoặc để chú ý rằng cách phân tích của các tác giả, vì phân tích trên số trung bình giữa các địa phương nên không thể dùng từ “tăng” mà chỉ có thể nói là “cao” hay “thấp”).
Nhưng rất tiếc các tác giả đã dựa vào các chỉ số trung bình (tính trong vòng 5 năm) cho từng địa phương để suy luận. Và, qua phân phân tích “mô phỏng” mà tôi vừa trình bày [3], kết luận rút ra từ một phân tích dựa vào chỉ số trung bình như thế rất dễ đi đến kết luận sai. Xin nhấn mạnh: tôi không nói rằng không có mối liên hệ giữa năng lực công nghệ và phát triển kinh tế; trong thực tế có thể mối liên hệ đó có thật nhưng tôi chỉ lưu ý về phương pháp phân tích không thích hợp và do đó kết quả từ phân tích cũng không phù hợp với thực tế.
Vấn đề logic
Vấn đề thứ nhất là một mối tương quan thống kê không hẳn phản ảnh một mối liên hệ nhân quả (cause-effect relationship). Địa phương có chỉ số phát triển kinh tế cao thường có chỉ số năng lực công nghệ cao. Nhưng điều đó không có nghĩa là năng lực công nghệ là nguyên nhân phát triển kinh tế (hay ngược lại). Có thể địa phương có thu nhập cao và chịu đầu tư vào khoa học và công nghệ, nhưng cũng có thể gia tăng đầu tư vàp công nghệ thúc đẩy phát triển kinh tế. Trong thực tế, rất khó mà phân biệt được con gà hay quả trứng có trước, và phân tích thống kê không cho phép một suy luận nhân quả. Dựa vào dữ liệu hiện nay, chúng ta chỉ có thể phát biểu rằng có một mối tương tác giữa phát triển kinh tế và năng lực công nghệ, nhưng kết quả phân tích không cho chúng ta biết cái nào là động lực và cái nào là hệ quả.
Một vấn đề logic khác liên quan đến khái niệm “ecologic fallacy” trong suy luận khoa học (tạm dịch là “sai lầm suy luận tổng quan”). Sai lầm suy luận tổng quan có nghĩa là sử dụng mối tương quan từ các quần thể để suy luận cho mối tương quan giữa các cá thể. Chẳng hạn như dựa vào quan sát rằng những nước tiêu thụ nhiều thực phẩm chứa chất béo có tỉ lệ ung thư vú cao, rồi suy luận rằng phụ nữ ăn nhiều thực phẩm chứa chất béo có nguy cơ mắc bệnh ung thư vú cao [4]. Đây là một sai lầm suy luận tổng quan khá tiêu biểu. Trong thực tế suy luận này có thể đúng, nhưng dựa vào số liệu trung bình từ các nước để làm cơ sở cho suy luận liên quan đến cá nhân là một suy luận yếu, một loại ngụy biện.
Liên quan đến suy luận tổng quan là khái niệm tương quan quần thể (ecologic correlation). Một trong những sai lầm tiêu biểu (và sau này trở thành một trường hợp trong sách giáo khoa về logic và thống kê học) là công trình nghiên cứu vào thập niên 1930s ở Mĩ về mối liên hệ giữa mù chữ và di dân. Trong nghiên cứu này các nhà nghiên cứu tính phần trăm dân số sinh đẻ ở nước ngoài, và phần trăm dân số biết đọc biết viết cho 48 tiểu bang [5]. Khi ứng dụng mô hình hồi qui tuyến tính, họ tìm thấy hệ số tương quan giữa hai chỉ số này là 0.53. Dựa vào hệ số tương quan này, các nhà nghiên cứu kết luận rằng người sinh đẻ ở nước ngoài có tỉ lệ biết chữ cao. Nhưng đây là một dạng tương quan quần thể, bởi vì đơn vị của phân tích không phải là những cá nhân mà là một quần thể. Sau này, các nhà thống kê phân tích lại dữ liệu, và phát hiện một mối tương quan nghịch đảo, với hệ số tương quan là −0.11; nói cách khác trong thực tế, người sinh đẻ ở nước ngoài có tỉ lệ mù chữ cao! Sở dĩ các nhà nghiên cứu có kết quả 0.53 là vì những người sinh đẻ ở nước ngoài thường định cư ở những tiểu bang mà người dân bản xứ có trình độ học vấn cao. Phân tích và suy luận dựa vào tương quan quần thể rất … nguy hiểm!
Quay trở lại với nghiên cứu về mối liên hệ giữa năng lực công nghệ và phát triển kinh tế, chúng ta thấy mối liên hệ mà các nhà nghiên cứu quan sát với hệ số tương quan R2 = 0,73 (hay hệ số tương quan là = 0,85). Nhưng đây là mối tương quan quần thể, chứ không phải cá thể. Chúng ta vẫn chưa biết nếu phân tích một cách thích hợp, hệ số tương quan này là bao nhiêu, nhưng dựa vào lí thuyết thống kê, rất dễ dàng thấy hệ số tương quan thật sẽ thấp hơn 0,85 rất nhiều.
Kết luận
Nói tóm lại, mối tương tác giữa năng lực công nghệ và phát triển kinh tế ở nước ta trong thời gian qua là một mối liên hệ phức tạp, nhưng những phân tích của các tác giả chưa đào sâu hay chưa “lột trần” được sự phức tạp của mối liên hệ đó. Vì chưa xem xét đến sự dao động trong từng địa phương nên tôi e rằng kết luận của các tác giả quá lạc quan so với thực tế.
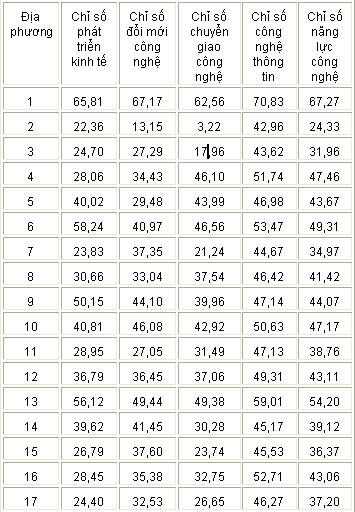
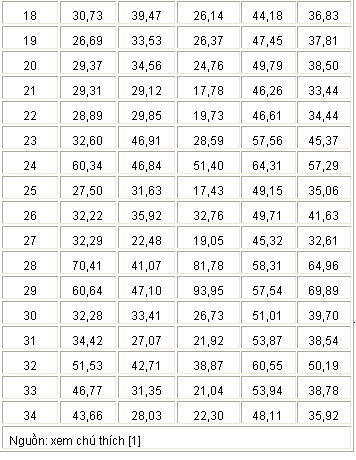
Như vừa trình bày trên, các tác giả quyết định tập trung vào phân tích các chỉ số bình quân giữa các địa phương là một cách đơn giả hóa vấn đề, và vì tính đơn giản như thế tôi nghĩ mô hình của các tác giả chưa phản ảnh đúng thực tế. Đứng trên quan điểm phương pháp học mà nói, dựa vào các chỉ số bình quân thường dẫn đến các ước số thiếu tính khách quan (biased) và thiếu nhất quán (inconsistency), hai đặc tính rất quan trọng trong phân tích thống kê. Sở dĩ có tình trạng này là vì chỉ số trung bình “che đậy” những dao động chung quanh con số trung bình. Chẳng hạn như chỉ số phát triển kinh tế của địa phương 1 là 65,81 (xem bảng 1), nhưng hai dãy số sau đây đều có thể cho ra một số trung bình như thế:
(a) 63,1 60,9 66,5 68,8 và 69,8 trung bình: 68,81
(b) 50,9 61,8 81,2 100,5 và 34,6 trung bình: 68,81
Giả dụ như (a) và (b) là chỉ số phát triển kinh tế của hai địa phương, chúng ta không thể nào kết luận rằng hai địa phương này có chỉ số phát triển tương đương nhau. Do đó, nếu chỉ tóm lược quá trình phát triển bằng chỉ số trung bình thì không thể nào phản ảnh được sự dao động (thậm chí khó so sánh được) chỉ số phát triển kinh tế của hai địa phương một cách khách quan. Đây cũng chính là một sai lầm cơ bản nhất của hệ số tương quan quần thể.
Một mô hình phân tích thích hợp phải sử dụng tất cả các số liệu cho từng năm và từng địa phương (chứ không phải chỉ đơn giản sử dụng số trung bình). Một trong những mô hình đó là mô hình phân tích đa tầng (multilevel analysis) [6]. Trong thời gian hai thập niên qua, với sự tiến bộ vượt bực của công suất máy tính, mô hình phân tích đa tầng có thể ứng dụng vào việc đánh giá những mối tương quan phức tạp và đa tầng một cách chính xác hơn. Hi vọng rằng bài viết ngắn này có thể giúp cho các tác giả có một cái nhìn mới hơn về dữ liệu mà các tác giả đã thu thập một cách công phu trong thời gian qua để đi đến một kết luận phù hợp với thực tế hơn.
Chú thích và tài liệu tham khảo:
Xin nói thêm rằng vì người viết không phải là nhà thống kê chuyên nghiệp nên một số thuật ngữ sử dụng trong bài viết có thể không chính xác, và những mô hình phân tích có thể có chỗ chưa hoàn chỉnh.
[1] Xem bài “Ứng dụng phương pháp kinh tế lượng trong đánh giá tác động của khoa học và công nghệ đối với phát triển kinh tế” của Giáo sư Tăng Văn Khiên và Tiến sĩ Tạ Doãn Trịnh, Tạp chí Hoạt động Khoa học, số tháng 2 năm 2008. Có thể xem toàn văn bài viết tại đây.
 |
[2] Trong bài báo, các tác giả cho báo cáo các ước số của mô hình hồi qui tuyến tính [1] trong Bảng 2 (của bài báo), nhưng khi phân tích lại số liệu tôi không có cùng kết quả về thông số a (intercept) như sau:
Trong bài báo các tác giả lí giải rằng vì 3 chỉ số doimoi (đổi mới công nghệ), chuyengiao (chuyển giao công nghệ) và cntt (công nghệ thông tin và truyền thông) tương quan với nhau (còn gọi là multicollinearity hay tương quan đa tuyến tính), nên họ phải phân tích riêng lẻ từng biến một. Tôi không đồng ý với nhận xét này. Sự hiện diện của tương quan đa tuyến tính có thể gây khó khăn cho việc đánh giá mức độ ảnh hưởng của từng chỉ số, nhưng “khó khăn” còn tùy thuộc vào hệ số tương quan giữa 3 chỉ số trên. Trước hết, chúng ta thử xem qua hệ số tương quan giữa 3 yếu tố doimoi, chuyengiao và cntt qua biểu đồ sau đây:
|
Biểu đồ chỉ mối tương quan đa chiều giữa chỉ số phát triển kinh tế, đổi mới công nghệ, chuyển giao công nghệ và công nghệ thông tin. Số liệu tính toán từ 34 địa phương. Đây là các hệ số tương quan quần thể (ecologic correlation) do đó cần phải cẩn thận trong diễn giải ý nghĩa của chúng. Các dấu đỏ chỉ ý nghĩa thống kê. |
Qua biểu đồ trên chúng ta thấy hệ số tương quan giữ doimoi vs chuyengiao = 0,67; giữa doimoi vs cntt = 0,74; và chuyengiao vs cntt = 0,65. Có thể nói đây là những hệ số tương quan khá cao. Nhưng chúng ảnh hưởng như thế nào đến mô hình hồi qui tuyến tính? Ảnh hưởng của mối tương quan đa chiều như thế thường thấy qua các ước số. Một trong những cách để xem xét ảnh hưởng của tương quan đa tuyến tính là ước tính hệ số lạm phát phương sai (variance inflation factor hay VIF). Theo thông lệ chung trong thống kê học, một yếu tố với VIF cao hơn 10 hay thấp hơn 0,1 được xem là có gây “khó khăn” cho mô hình. Do đó yếu tố nào có VIF từ 0,1 đến 10 có thể xem là chấp nhận được.
Tôi đã tiến hành phân tích mô hình đa biến sau đây: giả thiết chỉ số phát triển kinh tế là hàm số của 3 yếu tố doimoi, chuyengiao và cntt như sau:
kinhte = a + b×doimoi + c×chuyengiao + d×cntt + e
Kết quả ước tính các thông số a, b, c và d có thể xem trong bảng sau đây. Không có yếu tố nào có hệ số VIF cao hơn 10. Tất cả các yếu tố đều có ước số đúng với mối tương quan đơn biến (tức tất cả đều dương tính). Do đó, chúng ta có thể sử dụng mô hình hồi qui đa biến để phân tích. Tuy nhiên, qua phân tích trong bảng dưới đây, chúng ta dễ dàng thấy ảnh hưởng của đổi mới công nghệ không có ý nghĩa thống kê; chỉ có chuyển giao công nghệ và công nghệ thông tin và truyền thông có ảnh hưởng đến sự phát triển kinh tế giữa các địa phương.
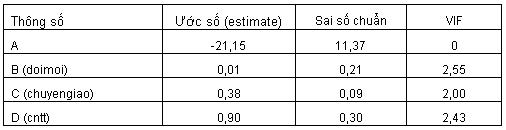 |
Mô hình đa biến này giải thích khoảng 75% khác biệt về chỉ số phát triển kinh tế giữa các địa phương.
Qua ước số của các thông số trong bảng trên, chúng ta còn thấy ảnh hưởng của doimoi không có ý nghĩa thống kê một khi xem xét ảnh hưởng của chuyengiao và cntt trong mô hình. Do đó, chúng ta có thể loại bỏ yếu tố doimoi, và mô hình trở thành đơn giản hơn như sau:
kinhte = -21,25 + 0,38×chuyengiao + 0,91×cntt
mô hình này “giải thích” 74% những khác biệt về chỉ số phát triển kinh tế giữa các địa phương. Nói cách khác, như chúng ta kì vọng, loại bỏ doimoi không có ảnh hưởng gì đến độ chính xác của mô hình. Tính theo hệ số xác định này, mô hình 2 biến là mô hình tối ưu nhất.
Câu hỏi đặt ra là giữa hai yếu tố này, yếu tố nào quan trọng hơn? Vì hai yếu tố có hai đơn vị đo lường khác nhau, nên không thể sử dụng thông số 0,38 để nói rằng chuyengiao kém quan trọng hơn cntt (0,91). Có thể sử dụng một số tính toán theo phương pháp “bootstrap” và thấy rằng trong tổng số R2 (74%), yếu tố chuyengiao giải thích 39% và cntt 35%. Như vậy, số liệu hiện nay cho thấy chuyển giao công nghệ có ảnh hưởng đến phát triển kinh tế lớn hơn ảnh hưởng của công nghệ thông tin. (Về phương pháp tính toán này có thể xem bài History and Use of Relative Importance Indices in Organizational Research của Johnson JW, và Lebreton JM, tập san Organizational Research Methods 2004; 7, 238–257)
Ngoài ra, không nhất thiết chúng ta phải tuân thủ theo phương trình về năng lực công nghệ mà các nước khác sử dụng, như
nangluc = doimoi/8 + chuyengiao*3/8 + cntt/2
mà có thể phát triển riêng một phương trình cho nước ta. Việc phát triển mô hình (hay phương trình) mới này cũng không khó khăn, nếu ứng dụng mô hình phân tích mà giới di truyền học hay gọi là principal component model. Nhưng đây là một lĩnh vực thú vị khác mà tôi chưa muốn bàn sâu thêm ở đây.
[3] Để chứng minh việc diễn giải từ phân tích dựa vào chỉ số trung bình có thể sai lầm, chúng ta tưởng tượng một nghiên cứu gồm 6 địa phương được thu thập qua năm năm. Số liệu về chỉ số phát triển kinh tế và năng lực công nghệ của 6 địa phương như sau (đây là số liệu do tôi “mô phỏng” thủ công):
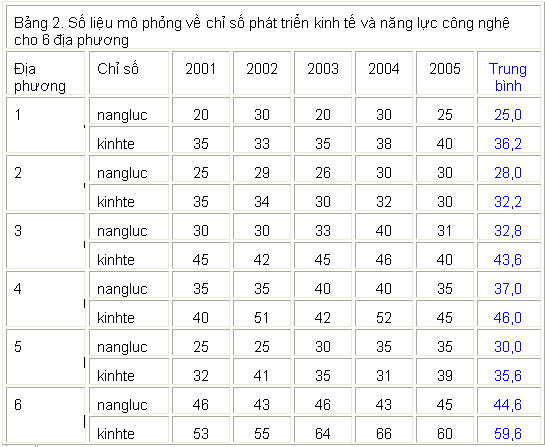 |
Vấn đề tương đối phức tạp hơn ở đây là chúng ta có số liệu 5 năm cho từng địa phương, và vì thế, chúng ta cần kí hiệu để chỉ các số liệu này. Gọi j là địa phương (j = 1, 2, …, 6), và t là năm (t = 2001, 2002, …, 2005). Chỉ số năng lực công nghệ và phát triển kinh tế cho từng địa phương j và năm t có thể kí hiệu bằng nanglucjt và kinhtejt. Với các kí hiệu này, chúng ta có thể phân tích cho từng địa phương qua mô mô hình hồi qui tuyến tính như sau:
Trong đó, aj và bj là hai thông số của mô hình cho từng địa phương j, và ejt là phần dư (residual). Mô hình trên còn có nghĩa là chúng ta phải phân tích mô hình 6 lần (cho 6 địa phương) để có được những thông số cần thiết. Kết quả phân tích như sau:
 |
Tức là, ở mỗi địa phương, không có mối liên hệ nào giữa nangluc và kinhte! Nói cách khác, năng lực công nghệ không có tác động gì đến phát triển kinh tế, và đây là kết luận đúng với thực tế.
Nhưng giả dụ rằng chúng ta bỏ qua sự dao động giữa các năm trong từng địa phương, mà chỉ tập trung vào chỉ số trung bình cho từng địa phương, và phân tích hai chỉ số này (cột sau cùng của bảng số liệu trên) thì kết quả sẽ ra sao? Biểu đồ sau đây sẽ cho thấy có một mối liên hệ rất chặt chẽ giữa chỉ số bình quân nangluc và kinhte.
Thật vậy, nếu ứng dụng mô hình hồi qui tuyến tính cho hai chỉ số trung bình trên, chúng ta sẽ có phương trình kinhte = -2,09 + 1,35×nangluc, với hệ số xác định R2 = 0,90! Nhưng chúng ta biết rằng trong thực tế thì khi chỉ số năng lực công nghệ tăng hay giảm chẳng có liên quan gì đến chỉ số phát triển kinh tế. Do đó, phân tích dựa vào các chỉ số quân bình cho chúng ta một kết quả rất sai lầm, và kết luận cũng rất sai lầm.
|
Biểu đồ 1: Mối liên hệ giữa chỉ số quân bình về năng lực công nghệ và phát triển kinh tế (số liệu mô phỏng). |
[4] Carroll K 1975 Experimental evidence of dietary factors and hormone-dependent cancers. Cancer Research 35: 3374–83
[5] Robinson W S 1950. Ecological correlations and the behavior of individuals. American Sociological Review 15: 351–57.
[6] Mô hình đa tầng có thể mô tả đơn giản như sau: Gọi j là địa phương (j = 1, 2, …, 6), và t là năm (t = 2001, 2002, …, 2005). Chỉ số năng lực công nghệ và phát triển kinh tế cho từng địa phương j và năm t có thể kí hiệu bằng nanglucjt và kinhtejt. Mô hình hồi qui đa tầng phát biểu như sau: chỉ số kinh tế của một địa phương của bất cứ năm nào bao gồm mức khởi đầu (tạm kí hiệu aj) và tỉ lệ tăng trưởng theo từng năm (kí hiệu là bt). Nói cách khác:
kinhtejt = aj + bj×nanglucjt + ejt
Mô hình trên cho từng địa phương j. Nói cách khác, mỗi địa phương khởi đầu với aj khác nhau và tỉ lệ tăng trưởng bj cũng khác nhau. Ngoài ra, giả thiết rằng aj bao gồm một chỉ số trung bình cho tất cả các địa phương (kí hiệu là a0) cộng/trừ cho ảnh hưởng của từng địa phương (dj0):
aj = a0 + dj0
Tương tự, tỉ lệ tăng trưởng bj bao gồm một chỉ số tăng trưởng trung bình cho tất cả các địa phương (kí hiệu là b0)cộng/trừ cho ảnh hưởng của từng địa phương (dj1):
bj = b0 + dj1
Thay thế hai phương trình này vào mô hình [2], chúng ta có:
kinhtejt = (a0 + b0×nanglucjt) + (dj0 + dj1×nanglucjt + ejt)
Chú ý trong mô hình trên có hai phần: phần đầu (a0 + b0×nanglucjt) còn được gọi là phần “fixed effects” (ảnh hưởng bất biến), và phần hai (dj0 + dj1×nanglucjt + ejt) là phần “random effects” (ảnh hưởng ngẫu nhiên). Có thể ước tính các thông số trong mô hình trên một cách dễ dàng bằng các phần mềm mới như R (xem “Phân tích số liệu và tạo biểu đồ bằng R” của Nguyễn Văn Tuấn, do Nhà xuất bản Khoa học Kỹ thuật phát hành năm 2007.
Bảng 1. Chỉ số bình quân về phát triển kinh tế, đổi mới công nghệ, chuyển giao công nghệ, và công nghệ thông tin của 34 tỉnh / thành trong thời gian 2001 – 2005.
|
|
Nguyễn Văn Tuấn