Topo của vũ trụ
Vấn đề nghiên cứu topo của vũ trụ đang gây chú ý của nhiều nhà vũ trụ học. Nhiều vũ trụ xét về mặt hình học là một vũ trụ vô hạn (infinite) song nếu chú ý đến topo (tức đến toàn cục) thì lại là một vũ trụ hữu hạn (finite). Nhiều quan sát CMB (Cosmic Microwave Background- Bức xạ Phông Vũ trụ) cũng được chính xác hóa thêm nhờ những chi tiết phát sinh từ những hệ quả topo. Bài viết này nhằm mục đích giới thiệu trong vài nét tổng quát ảnh hưởng của topo đến vũ trụ học.
Topo (topology) là gì?
Topo là môn học nghiên cứu hình dạng của một không gian về các mặt cơ bản nhất đó là tính liên thông (connectedness), tính liên tục (continuity) và các biên (boundary). Những tính này bất biến đối với các phép biến đổi liên tục gồm các biến đổi như kéo dài, uốn cong mà không bao gồm các biến đổi như xé rách (tearing) hoặc dán dính (gluing).
Xem hình 1 ta thấy một cái cốc, một hình xuyến và một hình xuyến xoắn là tương đương topo với nhau.
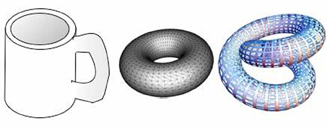 Hình 1. Cái cốc, hình xuyến và hình xuyến xoắn là tương đương topo với nhau. |
Quả thật như vậy chỉ cần các phép kéo dài và uốn cong ta có thể biến một hình xuyến thành một cái cốc (xem hình 2).
 Hình 2. Biến một hình xuyến thành cái cốc nhờ các phép biến đổi liên tục topo |
Hình học và topo
Cần phân biệt hình học (độ cong phẳng, dương hay âm?) và topo (dạng như thế nào, liên thông như thế nào?). Xét về mặt hình học có thể tồn tại 3 loại vũ trụ: vũ trụ phẳng (Euclidean, độ cong bằng không), vũ trụ cầu (đóng, hữu hạn và độ cong dương) và vũ trụ hyperbolic (mở, vô tận và độ cong âm), xem hình 3.
Khi nói đến độ cong âm người ta thường nghĩ đến một không gian vô hạn. Song có thể có nhiều độ cong trong một topo, ví dụ một hình xuyến (torus) có độ cong âm ở mặt trong (inside edge) mặc dầu nó là một topo hữu hạn (finite).
Thuyết tương đối tổng quát (với các phương trình Einstein vốn là những phương trình vi phân ) chỉ nói lên được tính định xứ (local) mà không thể xác định được tính toàn cục (global) tức topo của vũ trụ. Thuyết tương đối tổng quát không bất biến đối với các biến đổi đồng phôi (homeomorphism-xem chú thích) mà chỉ bất biến đối với các biến đổi vi phôi (diffeomorphism) tức các biến đổi tọa độ.
Với một vũ trụ đồng nhất và đẳng hướng ta có lời giải là metric Friedmann-Lemaitre-Robertson-Walker (FLRW):
ds2=gµvdxµdxv=-dt2+a2(η)[ dr2 + r2 (dθ2 + sin2θdΦ2)]
1 – kr2
trong đó a = thừa số kích thước của vũ trụ, độ cong k =0,+1,-1 tương ứng với độ cong bằng không, độ cong dương và độ cong âm (xem hình vẽ 3).
Giữa bán kính độ cong R và mật độ trung bình của vật chất trong vũ trụ có mối quan hệ R = a/|k|1/2 = 1/H|Ω-1|1/2, trong đó H = số Hubble, Ω = ρ/ρc còn ρc là mật độ ứng với vũ trụ phẳng. Ta có các vũ trụ với độ cong bằng không, độ cong dương và độ cong âm tương ứng với các mật độ Ω = 1, >1 và <1.
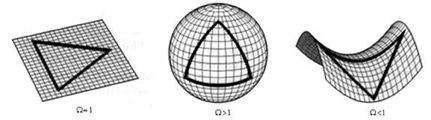 Hình 3 . Từ trái sang phải: độ cong phẳng, độ cong dương và độ cong âm |
Một yếu tố metric định xứ cho trước có thể tương ứng với một tập lớn mô hình vũ trụ khác nhau về mặt topo.
Tồn tại vô số (đếm được) những dạng không gian với độ cong dương, tất cả đều là những không gian đóng và vô số không gian với độ cong âm trong đó một số là không gian đóng (hữu hạn) một số là không gian mở (vô tận).
Thuyết tương đối mô tả một hình xuyến và một mặt phẳng với cùng những phương trình như nhau mặc dầu hình xuyến là hữu hạn trong khi mặt phẳng là vô hạn. Để xác định topo của vũ trụ cần những hiểu biết vật lý nằm ngoài lý thuyết tương đối (như CMB – Cosmic Microwave Background – Bức xạ Phông của Vũ trụ).
Hãy hình dung một buồng gương, đó là cái phòng với 6 bức tường (gồm cả trần và nền) là gương. Nếu chúng ta vào một phòng như thế với vài ngọn nến thì vì hệ quả phản chiếu trên các tường bằng gương chúng ta có cảm giác lọt vào một không gian vô tận.
Giống như trong một buồng gương (xem hình 4) sự vô tận của vũ trụ có thể chỉ là một ảo tưởng. Vũ trụ có thể hữu hạn trong thực tế. Ảo tưởng vô tận phát sinh từ hiện tượng tia sáng thực hiện một quỹ đạo chạy quanh không gian nhiều lần (khi vũ trụ là hữu hạn) và như thế tạo nên hình ảnh đa bội của từng thiên hà.
 Hình 4 . Buồng gương gây hệ quả vô tận của một đối tượng hữu hạn |
Nếu trong buồng kính ta có 3 quả bóng thì bức tranh tạo nên là hình ảnh của vô số quả bóng như trong hình 5.
 Hình 5. Ba quả bóng trong buồng kính tạo nên hình ảnh vô số quả bóng |
Buồng gương là hình tượng của một vũ trụ hữu hạn nhưng cho ảo tưởng vô tận. Lẽ dĩ nhiên vũ trụ không có biên để phản xạ ánh sáng song thay vì bị phản xạ như trong buồng gương thì ánh sáng có thể đi vòng quanh vũ trụ nhiều lần. Từ bức tranh các hình ảnh đa bội lặp lại người ta có thể suy ra kích thước và hình dáng thật sự của vũ trụ, tức xác định topo của vũ trụ.
Tạo một hình
Topo có thể giúp ta tạo một hình xuyến (hoặc một dải Moebius) từ một mảnh phẳng của không thời gian bằng cách đồng nhất các đường mép (edge) đối diện của mảnh phẳng này (xem hình 6).
Nói chung người ta biểu diễn một hình như phần trong của một đa diện (polyhedron) với các mặt đối nhau được đồng nhất từng đôi một.
Trên hình 6 ta thấy nếu dán 2 mép của một hình vuông ta có một hình trụ, nếu dán các mép (tức đồng nhất các mép a với a, b với b) của một hình vuông ta có một hình xuyến, nếu dán các mép của hình bát giác (đồng nhất a với a, b với b, c với c,…) ta có một hình xuyến với 2 lỗ. Ta gọi số lỗ là genus vậy ví dụ hình xuyến 2 lỗ có genus = 2.
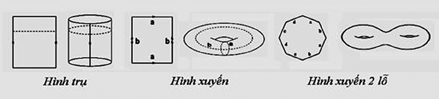 Hình 6. Tạo hình trụ, các hình xuyến 1 lỗ và 2 lỗ bằng cách dán các mép đối nhau (tức đồng nhất các mép) |
Chú ý hình xuyến S1x S1 có được nhờ đồng nhất các mép đối diện của một hình vuông là một không gian phẳng trong khi hình xuyến thông thường là không gian không phẳng. Song về mặt topo 2 hình xuyến này là tương đương.
Hình trụ, hình xuyến một lỗ, hai lỗ là những không gian topo đa liên thông (multiplyconnected). Trong hình 7 ta có một topo đơn liên thông (cột một) và hai topo đa liên thông (cột 2 và 3).
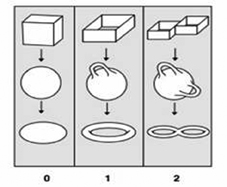 Hình 7. Đây là vài ví dụ của những đa tạp đồng phôi (homeomorphic) , những con số ở hàng dưới là số lỗ trong topo của chúng |
Phần trong của một đa diện 10 mặt ngũ giác mà từng đôi các mặt ngũ giác được đồng nhất với nhau sẽ là một không gian đóng với độ cong âm (compact hyperbolic space).
Vậy vấn đề nghiên cứu topo vũ trụ là nằm trong những câu hỏi sau đây.
Vũ trụ đóng hay mở? Vũ trụ có lỗ (hay tay quai-handle) không? Vũ trụ là liên thông hay đa liên thông? Những câu hỏi topo này thường bị bỏ quên bởi những nhà vũ trụ học. Trong một mô hình đầy đủ phải kể đến những câu hỏi topo này. Vũ trụ thực sự là sân khấu của những ảo tưởng quang học khổng lồ phát sinh vì những hiệu ứng thấu kính topo (topological lens).
Nghiên cứu vũ trụ ta phải chú ý hai mặt: hình học và topo. Về mặt hình học ta có: không gian Euclide (độ cong bằng không), không gian cầu (độ cong dương) và không gian hyperbolic (độ cong âm).
Không gian cầu trong mọi trường hợp là hữu hạn. Đối với hai loại không gian còn lại thì tính hữu hạn hoặc vô tận lại phụ thuộc vào topo. Nếu là topo đơn liên thông (simply-connected) thì chúng vô tận.
Song đối với topo đa liên thông (như hình xuyến với một lỗ hay hai lỗ) thì chúng ta có khả năng xét những mô hình vũ trụ trong đó không gian là hữu hạn bất kể độ cong là như thế nào ngay cả lúc mật độ vật chất và hằng số vũ trụ là rất thấp (mà nếu chỉ xét hình học thì ta phải có không gian phẳng hoặc hyperbolic vô tận).
Như vậy một không gian với độ cong âm có thể là hữu hạn nếu topo là đa liên thông.
Một vài chi tiết toán học
Trong khuôn khổ của vũ trụ học chuẩn thì vũ trụ được mô tả bởi một đa tạp không thời gian M4 = RxM cộng với metric FLRW. Trong đó M = E3 (Euclidean), S3 (cầu) hoặc H3 (không gian hyperbolic có hình một cái yên ngựa). Điều này thường dẫn đến một sự hiểu nhầm: độ cong của M là tất cả điều gì cần thiết để xác định xem không gian 3 chiều là hữu hạn (finite) hay vô hạn (infinite). Bởi vì không gian M có thể chỉ là một trong những đa tạp thương (quotient manifold) khả dĩ.
M= Mc / G
Trong đó Mc = (E3,S3,H3) là không gian gọi là không gian phủ tổng quát (universal covering). Không gian M là không gian đa liên thông. Phép G cho phép phủ Mc bằng những tế bào gọi là đa diện cơ bản (fundamental polyhedron-FP) và thực hiện những phép tịnh tiến gắn liền với việc đồng nhất các mép (xem hình 8).
Ví dụ hình xuyến T2=E2/G trong đó FP=là một hình chữ nhật với các mép đồng nhất như trên hình vẽ số 6.
Trong một không gian đa liên thông bất kỳ hai điểm nào cũng có thể được nối liền bởi nhiều hơn một đường trắc địa và hệ quả trong một vũ trụ hữu hạn ánh sáng từ một đối tượng có thể đến với một quan sát viên theo nhiều quỹ đạo khác nhau – và như thế trên bầu trời ta có nhiều hình ảnh của một nguồn bức xạ.
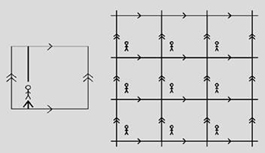 Hình 8.Cư dân trong FD và trong không gian phủ |
Ta lát không gian phủ tổng quát (universal covering) với nhiều FD bằng cách đồng nhất các mặt mép.
Một cư dân của hình xuyến khi nhìn về phía trước thấy phía sau của mình và nhìn thấy trong không gian phủ tổng quát một mạng các hình ảnh của mình. (xem hình 8).
Với những không gian đa liên thông (có một số lỗ ) số lượng N các bản copy của FD trong bức tranh quan sát vũ trụ có thể đánh giá bởi công thức: N=V/VFD. Trong đó V là thể tích của vùng vũ trụ quan sát được còn VFD là thể tích của FD.
Topo và CMB
Trong vũ trụ học CMB là bức xạ nhiệt tàn dư từ lúc Big Bang (xem hình 9).
CMB có thể giúp chúng ta xác định topo. Một phương pháp để làm việc đó là thực hiện mô hình toán học bằng máy tính của CMB đối với một topo nào đó rồi so sánh với quan trắc vũ trụ.
 Hình 9 . Bản đồ Bức xạ Phông Vũ trụ CMB trên bầu trời |
Tính đa liên thông được khai thác để tìm ra những bất thường trong phổ năng lượng do hệ quả topo. Một điểm bức xạ theo nhiều hướng khác nhau và ánh sáng sau khi đi vòng quanh vũ trụ nhiều lần sẽ đến người quan sát và cho chúng ta nhiều hình ảnh đa bội của điểm bức xạ.
Nhiều khía cạnh của CMB có thể bị thay đổi khi topo vũ trụ là đa liên thông (hữu hạn):
(1) Topo đa liên thông phá hủy tính đẳng hướng và tính đồng nhất toàn cục, xuất hiện trên CMB một phân bố bất đẳng hướng và bất đồng nhất ứng với các hình ảnh ảo (ghost) của nhiều điểm,
(2) Phổ các loại thăng giáng là gián đoạn, điều này phản ánh một không gian hữu hạn (tương tự như trong Cơ học lượng tử thể tích hữu hạn cho phổ năng lượng gián đoạn),
(3) Bức tranh các thăng giáng nhiệt độ phản ánh sự xuất hiện lặp lại của những điểm nóng và lạnh do hệ quả thấu kính topo.
Kết luận
Topo vũ trụ là một lĩnh vực quan trọng phối hợp các lý thuyết toán học với những định luật vật lý. Chúng ta có khả năng quan sát được topo vũ trụ một cách gián tiếp nhờ quan sát CMB. Hiểu được topo vũ trụ chúng ta có thể nghiên cứu chính xác hơn ảnh hưởng của năng-lượng vật chất lên không thời gian.Trong vũ trụ học hiện đại các nhà khoa học sử dụng toàn diện vật lý, hình học lẫn topo.
Dường như kết hợp lý thuyết và quan trắc các nhà vũ trụ học đối diện với hiện tượng một không gian với độ cong âm (mật độ vật chất thấp) lại có thể là hữu hạn về toàn cục và trong trường hợp đó ta phải có một topo đa liên thông. Thiên nhiên vốn kinh hãi cái vô cùng (Nature abhors an infininity).
—————-
Tài liệu tham khảo và chú thích
[1] Mark Baltovic, The topology of the Universe
[2] M.J.Reboucas, G.I.Gomero, Cosmic topology:A brief Overview, Brazilian Journal of Physics, vol.34, no.4A, December,2004
[3] Jean-Pierre Luminet, Is the Universe crumpled?
[4] Janna Levin, Topology and the Cosmic Microwave Background,
arXiv:gr-qc/0108043v2 20 Aug2001, Physics Reports 365(2002) 251-333
[5] Biến đổi đồng phôi là một biến đổi liên tục không chứa phép cắt và dán.
